In order for a single plane to be drawn through any three points in space, it is necessary that these points do not lie on the same straight line.

Consider the points M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2), M 3 (x 3, y 3, z 3) in the general Cartesian coordinate system.

In order for an arbitrary point M(x, y, z) to lie in the same plane with points M 1, M 2, M 3, it is necessary that the vectors be coplanar.

(
) = 0

Thus,

Equation of a plane passing through three points:

Equation of a plane given two points and a vector collinear to the plane.

Let the points M 1 (x 1,y 1,z 1),M 2 (x 2,y 2,z 2) and the vector be given
.

Let's create an equation for a plane passing through the given points M 1 and M 2 and an arbitrary point M (x, y, z) parallel to the vector .

Vectors
and vector
must be coplanar, i.e.

(
) = 0

Plane equation:

Equation of a plane using one point and two vectors,

collinear to the plane.

Let two vectors be given
And
, collinear planes. Then for an arbitrary point M(x, y, z) belonging to the plane, the vectors
must be coplanar.

Plane equation:

Equation of a plane by point and normal vector .

Theorem. If a point M is given in space 0 (X 0 , y 0 , z 0 ), then the equation of the plane passing through the point M 0 perpendicular to the normal vector (A, B, C) has the form:

A(x – x 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0.

Proof. For an arbitrary point M(x, y, z) belonging to the plane, we compose a vector. Because vector is the normal vector, then it is perpendicular to the plane, and, therefore, perpendicular to the vector
. Then the scalar product

= 0

Thus, we obtain the equation of the plane

The theorem has been proven.

Equation of a plane in segments.

If in the general equation Ax + Bi + Cz + D = 0 we divide both sides by (-D)

,

replacing
, we obtain the equation of the plane in segments:

The numbers a, b, c are the intersection points of the plane with the x, y, z axes, respectively.

Equation of a plane in vector form.

Where

- radius vector of the current point M(x, y, z),

A unit vector having the direction of a perpendicular dropped onto a plane from the origin.

,  and  are the angles formed by this vector with the x, y, z axes.

p is the length of this perpendicular.

In coordinates, this equation looks like:

xcos + ycos + zcos - p = 0.

Distance from a point to a plane.

The distance from an arbitrary point M 0 (x 0, y 0, z 0) to the plane Ax+By+Cz+D=0 is:

Example. Find the equation of the plane, knowing that point P(4; -3; 12) is the base of the perpendicular dropped from the origin to this plane.

So A = 4/13; B = -3/13; C = 12/13, we use the formula:

A(x – x 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0.

Example. Find the equation of a plane passing through two points P(2; 0; -1) and

Q(1; -1; 3) perpendicular to the plane 3x + 2y – z + 5 = 0.

Normal vector to the plane 3x + 2y – z + 5 = 0
parallel to the desired plane.

We get:

Example. Find the equation of the plane passing through points A(2, -1, 4) and

B(3, 2, -1) perpendicular to the plane X + at + 2z – 3 = 0.

The required equation of the plane has the form: A x+B y+C z+ D = 0, normal vector to this plane (A, B, C). Vector
(1, 3, -5) belongs to the plane. The plane given to us, perpendicular to the desired one, has a normal vector (1, 1, 2). Because points A and B belong to both planes, and the planes are mutually perpendicular, then

So the normal vector (11, -7, -2). Because point A belongs to the desired plane, then its coordinates must satisfy the equation of this plane, i.e. 112 + 71 - 24 +D= 0;D= -21.

In total, we get the equation of the plane: 11 x - 7y – 2z – 21 = 0.

Example. Find the equation of the plane, knowing that point P(4, -3, 12) is the base of the perpendicular dropped from the origin to this plane.

Finding the coordinates of the normal vector
= (4, -3, 12). The required equation of the plane has the form: 4 x – 3y + 12z+ D = 0. To find the coefficient D, we substitute the coordinates of point P into the equation:

16 + 9 + 144 + D = 0

In total, we get the required equation: 4 x – 3y + 12z – 169 = 0

Example. Given are the coordinates of the vertices of the pyramid A 1 (1; 0; 3), A 2 (2; -1; 3), A 3 (2; 1; 1),

Find the length of edge A 1 A 2.

Find the angle between edges A 1 A 2 and A 1 A 4.

Find the angle between edge A 1 A 4 and face A 1 A 2 A 3.

First we find the normal vector to the face A 1 A 2 A 3 How vector product vectors
And
.

= (2-1; 1-0; 1-3) = (1; 1; -2);

Let's find the angle between the normal vector and the vector
.

-4 – 4 = -8.

The desired angle  between the vector and the plane will be equal to  = 90 0 - .

Find the area of ​​face A 1 A 2 A 3.

Find the volume of the pyramid.

Find the equation of the plane A 1 A 2 A 3.

Let's use the formula for the equation of a plane passing through three points.

2x + 2y + 2z – 8 = 0

x + y + z – 4 = 0;

When using the computer version “ Higher mathematics course” you can run a program that will solve the above example for any coordinates of the vertices of the pyramid.

To start the program, double-click on the icon:

In the program window that opens, enter the coordinates of the vertices of the pyramid and press Enter. In this way, all decision points can be obtained one by one.

Note: To run the program, the Maple program ( Waterloo Maple Inc.) of any version, starting with MapleV Release 4, must be installed on your computer.

Let us consider the plane Q in space. Its position is completely determined by specifying the vector N perpendicular to this plane and some fixed point lying in the Q plane. The vector N perpendicular to the Q plane is called the normal vector of this plane. If we denote by A, B and C the projections of the normal vector N, then

Let us derive the equation of the plane Q passing through a given point and having a given normal vector . To do this, consider a vector connecting a point with an arbitrary point on the Q plane (Fig. 81).

For any position of point M on the plane Q, the vector MHM is perpendicular to the normal vector N of the plane Q. Therefore, the scalar product Let us write the scalar product in terms of projections. Since , and is a vector, then

and therefore

We have shown that the coordinates of any point in the Q plane satisfy equation (4). It is easy to see that the coordinates of points not lying on the Q plane do not satisfy this equation (in the latter case ). Consequently, we have obtained the required equation for the plane Q. Equation (4) is called the equation of the plane passing through a given point. It is of the first degree relative to the current coordinates

So, we have shown that every plane corresponds to an equation of the first degree with respect to the current coordinates.

Example 1. Write the equation of a plane passing through a point perpendicular to the vector.

Solution. Here . Based on formula (4) we obtain

or, after simplification,

By giving the coefficients A, B and C of equation (4) different values, we can obtain the equation of any plane passing through the point . The set of planes passing through a given point is called a bundle of planes. Equation (4), in which the coefficients A, B and C can take any values, is called the equation of a bunch of planes.

Example 2. Create an equation for a plane passing through three points (Fig. 82).

Solution. Let's write the equation for a bunch of planes passing through the point

If all numbers A, B, C and D are different from zero, then the general equation of the plane is called complete. Otherwise, the general equation of the plane is called incomplete.

Let us consider all possible general incomplete equations of the plane in the rectangular coordinate system Oxyz in three-dimensional space.

Let D = 0, then we have a general incomplete plane equation of the form . This plane in the rectangular coordinate system Oxyz passes through the origin. Indeed, when substituting the coordinates of a point into the resulting incomplete equation of the plane, we arrive at the identity .

For , or , or we have general incomplete equations of the planes , or , or , respectively. These equations define planes parallel to the coordinate planes Oxy, Oxz and Oyz, respectively (see the article for the condition of parallel planes) and passing through the points and correspondingly. At. Since the point belongs to the plane by condition, then the coordinates of this point must satisfy the equation of the plane, that is, the equality must be true. From here we find. Thus, the required equation has the form .

Let us present the second way to solve this problem.

Since the plane, the general equation of which we need to compose, is parallel to the plane Oyz, then as its normal vector we can take the normal vector of the plane Oyz. The normal vector of the coordinate plane Oyz is the coordinate vector. Now we know the normal vector of the plane and the point of the plane, therefore, we can write its general equation (we solved a similar problem in the previous paragraph of this article):
, then its coordinates must satisfy the equation of the plane. Therefore, the equality is true where we find it from. Now we can write the desired general equation of the plane, it has the form .

Answer:

Bibliography.

• Bugrov Ya.S., Nikolsky S.M. Higher mathematics. Volume one: elements of linear algebra and analytical geometry.
• Ilyin V.A., Poznyak E.G. Analytic geometry.

ANGLE BETWEEN PLANES

Consider two planes α 1 and α 2, defined respectively by the equations:

Under angle between two planes we will understand one of the dihedral angles formed by these planes. It is obvious that the angle between the normal vectors and planes α 1 and α 2 is equal to one of the indicated adjacent dihedral angles or . That's why . Because And , That

.

Example. Determine the angle between planes x+2y-3z+4=0 and 2 x+3y+z+8=0.

Condition for parallelism of two planes.

Two planes α 1 and α 2 are parallel if and only if their normal vectors are parallel, and therefore .

So, two planes are parallel to each other if and only if the coefficients of the corresponding coordinates are proportional:

or

Condition of perpendicularity of planes.

It is clear that two planes are perpendicular if and only if their normal vectors are perpendicular, and therefore, or .

Thus, .

Examples.

STRAIGHT IN SPACE.

VECTOR EQUATION FOR A LINE.

PARAMETRIC DIRECT EQUATIONS

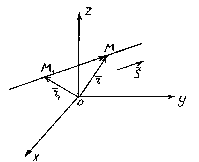
The position of a line in space is completely determined by specifying any of its fixed points M 1 and a vector parallel to this line.

A vector parallel to a line is called guides vector of this line.

So let the straight line l passes through a point M 1 (x 1 , y 1 , z 1), lying on a line parallel to the vector .

Consider an arbitrary point M(x,y,z) on a straight line. From the figure it is clear that .

Vectors and are collinear, so there is such a number t, what , where is the multiplier t can take any numeric value depending on the position of the point M on a straight line. Factor t called a parameter. Having designated the radius vectors of points M 1 and M respectively, through and , we obtain . This equation is called vector equation of a straight line. It shows that for each parameter value t corresponds to the radius vector of some point M, lying on a straight line.

Let's write this equation in coordinate form. Notice, that , and from here

The resulting equations are called parametric equations of a straight line.

When changing a parameter t coordinates change x, y And z and period M moves in a straight line.

CANONICAL EQUATIONS OF THE DIRECT

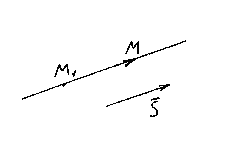
Let M 1 (x 1 , y 1 , z 1) – a point lying on a straight line l, And is its direction vector. Let us again take an arbitrary point on the line M(x,y,z) and consider the vector .

It is clear that the vectors are also collinear, so their corresponding coordinates must be proportional, therefore,

– canonical equations of a straight line.

Note 1. Note that the canonical equations of the line could be obtained from the parametric ones by eliminating the parameter t. Indeed, from the parametric equations we obtain or .

Example. Write down the equation of the line in parametric form.

Let's denote , from here x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Note 2. Let the straight line be perpendicular to one of the coordinate axes, for example the axis Ox. Then the direction vector of the line is perpendicular Ox, hence, m=0. Consequently, the parametric equations of the line will take the form

Excluding the parameter from the equations t, we obtain the equations of the line in the form

However, in this case too, we agree to formally write the canonical equations of the line in the form . Thus, if the denominator of one of the fractions is zero, this means that the straight line is perpendicular to the corresponding coordinate axis.

Similar to the canonical equations corresponds to a straight line perpendicular to the axes Ox And Oy or parallel to the axis Oz.

Examples.

GENERAL EQUATIONS OF A STRAIGHT LINE AS LINES OF INTERSECTION OF TWO PLANES

Through every straight line in space there are countless planes. Any two of them, intersecting, define it in space. Consequently, the equations of any two such planes, considered together, represent the equations of this line.

In general, any two non-parallel planes given by the general equations

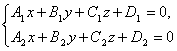
determine the straight line of their intersection. These equations are called general equations straight.

Examples.

Construct a line given by the equations

To construct a straight line, it is enough to find any two of its points. The easiest way is to select the points of intersection of a straight line with coordinate planes. For example, the point of intersection with the plane xOy we obtain from the equations of the straight line, assuming z= 0:

Having solved this system, we find the point M 1 (1;2;0).

Similarly, assuming y= 0, we get the point of intersection of the line with the plane xOz:

From the general equations of a straight line one can move on to its canonical or parametric equations. To do this you need to find some point M 1 on a straight line and the direction vector of a straight line.

Point coordinates M 1 we obtain from this system of equations, giving one of the coordinates an arbitrary value. To find the direction vector, note that this vector must be perpendicular to both normal vectors And . Therefore, beyond the direction vector of the straight line l you can take the vector product of normal vectors:

.

Example. Give general equations of the line to the canonical form.

Let's find a point lying on a line. To do this, we choose arbitrarily one of the coordinates, for example, y= 0 and solve the system of equations:

The normal vectors of the planes defining the line have coordinates Therefore, the direction vector will be straight

. Hence, l: .

ANGLE BETWEEN STRAIGHTS

Angle between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two lines be given in space:

Obviously, the angle φ between straight lines can be taken as the angle between their direction vectors and . Since , then using the formula for the cosine of the angle between vectors we get

This article gives an idea of ​​how to create an equation for a plane passing through a given point in three-dimensional space perpendicular to a given line. Let us analyze the given algorithm using the example of solving typical problems.

Finding the equation of a plane passing through a given point in space perpendicular to a given line

Let a three-dimensional space and a rectangular coordinate system O x y z be given in it. Point M 1 (x 1, y 1, z 1), line a and plane α passing through point M 1 perpendicular to line a are also given. It is necessary to write down the equation of the plane α.

Before we begin solving this problem, let us remember the geometry theorem from the syllabus for grades 10-11, which says:

Definition 1

Through a given point in three-dimensional space there passes a single plane perpendicular to a given straight line.

Now let's look at how to find the equation of this single plane passing through the starting point and perpendicular to the given line.

It is possible to write down the general equation of a plane if the coordinates of a point belonging to this plane are known, as well as the coordinates of the normal vector of the plane.

The conditions of the problem give us the coordinates x 1, y 1, z 1 of the point M 1 through which the plane α passes. If we determine the coordinates of the normal vector of the plane α, then we will be able to write down the required equation.

The normal vector of the plane α, since it is non-zero and lies on the line a, perpendicular to the plane α, will be any direction vector of the line a. Thus, the problem of finding the coordinates of the normal vector of the plane α is transformed into the problem of determining the coordinates of the directing vector of the straight line a.

Determining the coordinates of the direction vector of straight line a can be carried out by different methods: it depends on the option of specifying straight line a in the initial conditions. For example, if straight line a in the problem statement is given by canonical equations of the form

x - x 1 a x = y - y 1 a y = z - z 1 a z

or parametric equations type:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

then the direction vector of the straight line will have coordinates a x, a y and a z. In the case when straight line a is represented by two points M 2 (x 2, y 2, z 2) and M 3 (x 3, y 3, z 3), then the coordinates of the direction vector will be determined as (x3 – x2, y3 – y2 , z3 – z2).

Definition 2

Algorithm for finding the equation of a plane passing through a given point perpendicular to a given line:

We determine the coordinates of the direction vector of straight line a: a → = (a x, a y, a z) ;

We define the coordinates of the normal vector of the plane α as the coordinates of the directing vector of the straight line a:

n → = (A , B , C) , where A = a x , B = a y , C = a z;

We write the equation of the plane passing through the point M 1 (x 1, y 1, z 1) and having a normal vector n → = (A, B, C) in the form A (x – x 1) + B (y – y 1) + C (z – z 1) = 0. This will be the required equation of a plane that passes through a given point in space and is perpendicular to a given line.

The resulting general equation of the plane is: A (x – x 1) + B (y – y 1) + C (z – z 1) = 0 makes it possible to obtain the equation of the plane in segments or the normal equation of the plane.

Let's solve several examples using the algorithm obtained above.

Example 1

A point M 1 (3, - 4, 5) is given, through which the plane passes, and this plane is perpendicular to the coordinate line O z.

Solution

the direction vector of the coordinate line O z will be the coordinate vector k ⇀ = (0, 0, 1). Therefore, the normal vector of the plane has coordinates (0, 0, 1). Let us write the equation of a plane passing through a given point M 1 (3, - 4, 5), the normal vector of which has coordinates (0, 0, 1):

A (x - x 1) + B (y - y 1) + C (z - z 1) = 0 ⇔ ⇔ 0 (x - 3) + 0 (y - (- 4)) + 1 (z - 5) = 0 ⇔ z - 5 = 0

Answer: z – 5 = 0 .

Let's consider another way to solve this problem:

Example 2

A plane that is perpendicular to the line O z will be given by an incomplete general plane equation of the form C z + D = 0, C ≠ 0. Let us determine the values ​​of C and D: those at which the plane passes through a given point. Let's substitute the coordinates of this point into the equation C z + D = 0, we get: C · 5 + D = 0. Those. numbers, C and D are related by the relation - D C = 5. Taking C = 1, we get D = - 5.

Let's substitute these values ​​into the equation C z + D = 0 and get the required equation of a plane perpendicular to the straight line O z and passing through the point M 1 (3, - 4, 5).

It will look like: z – 5 = 0.

Answer: z – 5 = 0 .

Example 3

Write an equation for a plane passing through the origin and perpendicular to the line x - 3 = y + 1 - 7 = z + 5 2

Solution

Based on the conditions of the problem, it can be argued that the direction vector of a given straight line can be taken as the normal vector n → of a given plane. Thus: n → = (- 3 , - 7 , 2) . Let us write the equation of a plane passing through point O (0, 0, 0) and having a normal vector n → = (- 3, - 7, 2):

3 (x - 0) - 7 (y - 0) + 2 (z - 0) = 0 ⇔ - 3 x - 7 y + 2 z = 0

We have obtained the required equation of a plane passing through the origin of coordinates perpendicular to a given line.

Answer:- 3 x - 7 y + 2 z = 0

Example 4

A rectangular coordinate system O x y z is given in three-dimensional space, in it there are two points A (2, - 1, - 2) and B (3, - 2, 4). The plane α passes through point A perpendicular to the line A B. It is necessary to create an equation for the plane α in segments.

Solution

The plane α is perpendicular to the line A B, then the vector A B → will be the normal vector of the plane α. The coordinates of this vector are defined as the difference between the corresponding coordinates of points B (3, - 2, 4) and A (2, - 1, - 2):

A B → = (3 - 2 , - 2 - (- 1) , 4 - (- 2)) ⇔ A B → = (1 , - 1 , 6)

General equation plane will be written in the following form:

1 x - 2 - 1 y - (- 1 + 6 (z - (- 2)) = 0 ⇔ x - y + 6 z + 9 = 0

Now let’s compose the required equation of the plane in segments:

x - y + 6 z + 9 = 0 ⇔ x - y + 6 z = - 9 ⇔ x - 9 + y 9 + z - 3 2 = 1

Answer:x - 9 + y 9 + z - 3 2 = 1

It should also be noted that there are problems whose requirement is to write an equation of a plane passing through a given point and perpendicular to two given planes. In general, the solution to this problem is to construct an equation for a plane passing through a given point perpendicular to a given line, because two intersecting planes define a straight line.

Example 5

A rectangular coordinate system O x y z is given, in it there is a point M 1 (2, 0, - 5). The equations of two planes 3 x + 2 y + 1 = 0 and x + 2 z – 1 = 0, which intersect along straight line a, are also given. It is necessary to create an equation for a plane passing through point M 1 perpendicular to straight line a.

Solution

Let's determine the coordinates of the directing vector of the straight line a. It is perpendicular to both the normal vector n 1 → (3, 2, 0) of the n → (1, 0, 2) plane and the normal vector 3 x + 2 y + 1 = 0 of the x + 2 z - 1 = 0 plane.

Then, as the directing vector α → line a, we take the vector product of the vectors n 1 → and n 2 →:

a → = n 1 → × n 2 → = i → j → k → 3 2 0 1 0 2 = 4 i → - 6 j → - 2 k → ⇒ a → = (4 , - 6 , - 2 )

Thus, the vector n → = (4, - 6, - 2) will be the normal vector of the plane perpendicular to the line a. Let us write down the required equation of the plane:

4 (x - 2) - 6 (y - 0) - 2 (z - (- 5)) = 0 ⇔ 4 x - 6 y - 2 z - 18 = 0 ⇔ ⇔ 2 x - 3 y - z - 9 = 0

Answer: 2 x - 3 y - z - 9 = 0

If you notice an error in the text, please highlight it and press Ctrl+Enter