One of the sub-items of the topic “The equation of a straight line on a plane” is the issue of compiling parametric equations of a straight line on a plane in a rectangular coordinate system. The article below discusses the principle of compiling such equations for certain known data. Let us show how to pass from parametric equations to equations of a different form; Let's analyze the solution of typical problems.

A particular line can be defined by specifying a point that belongs to that line and a direction vector for the line.

Suppose we are given a rectangular coordinate system O x y . And also the straight line a is given, indicating the point M 1 lying on it (x 1, y 1) and the direction vector of the given straight line a → = (a x , a y) . We give a description of the given line a using equations.

We use an arbitrary point M (x, y) and get a vector M 1 M →; calculate its coordinates from the coordinates of the start and end points: M 1 M → = (x - x 1 , y - y 1) . Let's describe the result: the line is given by a set of points M (x, y), passes through the point M 1 (x 1, y 1) and has a direction vector a → = (a x , a y) . The specified set defines a straight line only when the vectors M 1 M → = (x - x 1 , y - y 1) and a → = (a x , a y) are collinear.

There is a necessary and sufficient condition for the collinearity of vectors, which in this case for the vectors M 1 M → = (x - x 1 , y - y 1) and a → = (a x , a y) can be written as an equation:

M 1 M → = λ · a → , where λ is some real number.

Definition 1

The equation M 1 M → = λ · a → is called the vector-parametric equation of the line.

In coordinate form, it looks like:

M 1 M → = λ a → ⇔ x - x 1 = λ a x y - y 1 = λ a y ⇔ x = x 1 + a x λ y = y 1 + a y λ

The equations of the resulting system x = x 1 + a x · λ y = y 1 + a y · λ are called parametric equations of a straight line on a plane in a rectangular coordinate system. The essence of the name is as follows: the coordinates of all points of a straight line can be determined by parametric equations on a plane of the form x = x 1 + a x λ y = y 1 + a y λ when iterating over all real values ​​of the parameter λ

According to the above, the parametric equations of a straight line on the plane x \u003d x 1 + a x λ y \u003d y 1 + a y λ determine a straight line that is given in a rectangular coordinate system, passes through the point M 1 (x 1, y 1) and has a guide vector a → = (a x , a y) . Therefore, if the coordinates of a certain point of the straight line and the coordinates of its directing vector are given, then it is possible to immediately write down the parametric equations of the given straight line.

Example 1

It is necessary to compose parametric equations of a straight line on a plane in a rectangular coordinate system, if the point M 1 (2, 3) belonging to it and its direction vector are given a → = (3 , 1) .

Solution

Based on the initial data, we get: x 1 \u003d 2, y 1 \u003d 3, a x \u003d 3, a y \u003d 1. The parametric equations will look like:

x = x 1 + a x λ y = y 1 + a y λ ⇔ x = 2 + 3 λ y = 3 + 1 λ ⇔ x = 2 + 3 λ y = 3 + λ

Let's clearly illustrate:

Answer: x = 2 + 3 λ y = 3 + λ

It should be noted: if the vector a → = (a x , a y) serves as a directing vector of the straight line a, and the points M 1 (x 1, y 1) and M 2 (x 2, y 2) belong to this line, then it can be determined by setting parametric equations of the form: x = x 1 + a x λ y = y 1 + a y λ , as well as this option: x = x 2 + a x λ y = y 2 + a y λ .

For example, we are given a directing vector of a straight line a → \u003d (2, - 1), as well as points M 1 (1, - 2) and M 2 (3, - 3) belonging to this line. Then the straight line is determined by parametric equations: x = 1 + 2 · λ y = - 2 - λ or x = 3 + 2 · λ y = - 3 - λ .

Attention should also be paid to the following fact: if a → = (a x , a y) is the directing vector of the straight line a , then any of the vectors will also be its directing vector μ a → = (μ a x , μ a y) , where μ ϵ R , μ ≠ 0 .

Thus, a straight line a on a plane in a rectangular coordinate system can be defined by parametric equations: x = x 1 + μ a x λ y = y 1 + μ a y λ for any non-zero value of μ.

Suppose the line a is given by the parametric equations x = 3 + 2 λ y = - 2 - 5 λ . Then a → = (2 , - 5) - direction vector of this line. And also any of the vectors μ · a → = (μ · 2 , μ · - 5) = 2 μ , - 5 μ , μ ∈ R , μ ≠ 0 will become the direction vector for the given straight line. For clarity, consider a specific vector - 2 · a → = (- 4 , 10) , it corresponds to the value μ = - 2 . In this case, the given straight line can also be determined by the parametric equations x = 3 - 4 · λ y = - 2 + 10 · λ .

Transition from parametric equations of a straight line on a plane to other equations of a given straight line and vice versa

In solving some problems, the use of parametric equations is not the most the best option, then it becomes necessary to translate the parametric equations of a straight line into equations of a straight line of a different form. Let's see how to do it.

Parametric equations of the straight line x = x 1 + a x · λ y = y 1 + a y · λ will correspond to the canonical equation of the straight line on the plane x - x 1 a x = y - y 1 a y .

We solve each of the parametric equations with respect to the parameter λ, equate the right parts of the obtained equalities and obtain the canonical equation of the given straight line:

x = x 1 + a x λ y = y 1 + a y λ ⇔ λ = x - x 1 a x λ = y - y 1 a y ⇔ x - x 1 a x = y - y 1 a y

In this case, it should not be embarrassing if a x or a y will be equal to zero.

Example 2

It is necessary to carry out the transition from the parametric equations of the straight line x = 3 y = - 2 - 4 · λ to the canonical equation.

Solution

We write the given parametric equations in the following form: x = 3 + 0 λ y = - 2 - 4 λ

We express the parameter λ in each of the equations: x = 3 + 0 λ y = - 2 - 4 λ ⇔ λ = x - 3 0 λ = y + 2 - 4

We equate the right parts of the system of equations and obtain the required canonical equation of a straight line in the plane:

x - 3 0 = y + 2 - 4

Answer: x - 3 0 = y + 2 - 4

In the case when it is necessary to write down the equation of the straight line of the form A x + B y + C = 0 , while the parametric equations of the straight line on the plane are given, it is necessary first to make the transition to the canonical equation, and then to the general equation of the straight line. Let's write down the whole sequence of actions:

x = x 1 + a x λ y = y 1 + a y λ ⇔ λ = x - x 1 a x λ = y - y 1 a y ⇔ x - x 1 a x = y - y 1 a y ⇔ ⇔ a y (x - x 1) = a x (y - y 1) ⇔ A x + B y + C = 0

Example 3

It is necessary to write down the general equation of a straight line if the parametric equations defining it are given: x = - 1 + 2 λ y = - 3 λ

Solution

First, let's make the transition to the canonical equation:

x = - 1 + 2 λ y = - 3 λ ⇔ λ = x + 1 2 λ = y - 3 ⇔ x + 1 2 = y - 3

The resulting proportion is identical to the equality - 3 · (x + 1) = 2 · y. Let's open the brackets and get the general equation of the straight line: - 3 x + 1 = 2 y ⇔ 3 x + 2 y + 3 = 0 .

Answer: 3x + 2y + 3 = 0

Following the above logic of actions, to obtain the equation of a straight line with slope factor, the equation of a straight line in segments or the normal equation of a straight line, it is necessary to obtain the general equation of a straight line, and from it to carry out a further transition.

Now consider the reverse action: writing the parametric equations of a straight line for a different given form of the equations of this straight line.

The easiest transition: from the canonical equation to the parametric ones. Let the canonical equation of the form be given: x - x 1 a x = y - y 1 a y . We take each of the relations of this equality equal to the parameter λ:

x - x 1 a x = y - y 1 a y = λ ⇔ λ = x - x 1 a x λ = y - y 1 a y

Let us solve the resulting equations for the variables x and y:

x = x 1 + a x λ y = y 1 + a y λ

Example 4

It is necessary to write down the parametric equations of the straight line if the canonical equation of the straight line on the plane is known: x - 2 5 = y - 2 2

Solution

Let's equate the parts of the known equation to the parameter λ: x - 2 5 = y - 2 2 = λ . From the obtained equality we obtain the parametric equations of the straight line: x - 2 5 = y - 2 2 = λ ⇔ λ = x - 2 5 λ = y - 2 5 ⇔ x = 2 + 5 λ y = 2 + 2 λ

Answer: x = 2 + 5 λ y = 2 + 2 λ

When it is necessary to make a transition to parametric equations from a given general equation of a straight line, an equation of a straight line with a slope or an equation of a straight line in segments, it is necessary to bring the original equation to the canonical one, and then make the transition to parametric equations.

Example 5

It is necessary to write down the parametric equations of the straight line with the known general equation of this straight line: 4 x - 3 y - 3 = 0 .

Solution

We transform the given general equation into an equation of the canonical form:

4 x - 3 y - 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4

We equate both parts of the equality to the parameter λ and obtain the required parametric equations of the straight line:

x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 λ y = - 1 3 + 4 λ

Answer: x = 3 λ y = - 1 3 + 4 λ

Examples and problems with parametric equations of a straight line on a plane

Let us consider the most common types of problems using parametric equations of a straight line on a plane in a rectangular coordinate system.

1. In problems of the first type, the coordinates of points are given, whether or not they belong to a straight line described by parametric equations.

The solution of such problems is based on the following fact: the numbers (x, y) determined from the parametric equations x \u003d x 1 + a x λ y \u003d y 1 + a y λ for some real value λ are the coordinates of a point belonging to the straight line, which is described these parametric equations.

Example 6

It is necessary to determine the coordinates of a point that lies on a straight line given by the parametric equations x = 2 - 1 6 · λ y = - 1 + 2 · λ for λ = 3 .

Solution

We substitute the known value λ = 3 into the given parametric equations and calculate the desired coordinates: x = 2 - 1 6 3 y = - 1 + 2 3 ⇔ x = 1 1 2 y = 5

Answer: 1 1 2 , 5

The following problem is also possible: let some point M 0 (x 0, y 0) be given on the plane in a rectangular coordinate system and it is necessary to determine whether this point belongs to the line described by the parametric equations x = x 1 + a x λ y = y 1 + a y λ .

To solve such a problem, it is necessary to substitute the coordinates of a given point into the known parametric equations of a straight line. If it is determined that such a value of the parameter λ = λ 0 is possible, at which both parametric equations will be true, then the given point belongs to the given straight line.

Example 7

Points M 0 (4, - 2) and N 0 (- 2, 1) are given. It is necessary to determine whether they belong to the straight line defined by the parametric equations x = 2 · λ y = - 1 - 1 2 · λ .

Solution

We substitute the coordinates of the point M 0 (4, - 2) into the given parametric equations:

4 = 2 λ - 2 = - 1 - 1 2 λ ⇔ λ = 2 λ = 2 ⇔ λ = 2

We conclude that the point M 0 belongs to a given line, because corresponds to the value λ = 2 .

2 = 2 λ 1 = - 1 - 1 2 λ ⇔ λ = - 1 λ = - 4

It is obvious that there is no such parameter λ to which the point N 0 will correspond. In other words, the given line does not pass through the point N 0 (- 2 , 1) .

Answer: point M 0 belongs to a given line; the point N 0 does not belong to the given line.

1. In problems of the second type, it is required to compose parametric equations of a straight line on a plane in a rectangular coordinate system. The simplest example of such a problem (with known coordinates of the point of the line and direction vector) was considered above. Now let's look at examples in which you first need to find the coordinates of the direction vector, and then write down the parametric equations.

Example 8

Point M 1 1 2 , 2 3 is given. It is necessary to compose parametric equations of a straight line passing through this point and a parallel straight line x 2 \u003d y - 3 - 1.

Solution

According to the condition of the problem, the straight line, the equation of which we have to get ahead of, is parallel to the straight line x 2 \u003d y - 3 - 1. Then, as a directing vector of a straight line passing through a given point, it is possible to use the directing vector of a straight line x 2 = y - 3 - 1, which we write in the form: a → = (2, - 1) . Now all the necessary data are known in order to compose the desired parametric equations:

x = x 1 + a x λ y = y 1 + a y λ ⇔ x = 1 2 + 2 λ y = 2 3 + (- 1) λ ⇔ x = 1 2 + x λ y = 2 3 - λ

Answer: x = 1 2 + x λ y = 2 3 - λ .

Example 9

Point M 1 (0, - 7) is given. It is necessary to write the parametric equations of a straight line passing through this point perpendicular to the straight line 3 x – 2 y – 5 = 0 .

Solution

As the directing vector of the straight line, the equation of which must be composed, it is possible to take the normal vector of the straight line 3 x - 2 y - 5 = 0 . Its coordinates are (3 , - 2) . We write the required parametric equations of the straight line:

x = x 1 + a x λ y = y 1 + a y λ ⇔ x = 0 + 3 λ y = - 7 + (- 2) λ ⇔ x = 3 λ y = - 7 - 2 λ

Answer: x = 3 λ y = - 7 - 2 λ

1. In problems of the third type, it is required to make a transition from parametric equations of a given straight line to other types of equations that determine it. We considered the solution of such examples above, we will give one more.

Example 10

Given a straight line on a plane in a rectangular coordinate system, defined by the parametric equations x = 1 - 3 4 · λ y = - 1 + λ . It is necessary to find the coordinates of some normal vector of this line.

Solution

To determine the desired coordinates of the normal vector, we will make the transition from parametric equations to the general equation:

x = 1 - 3 4 λ y = - 1 + λ ⇔ λ = x - 1 - 3 4 λ = y + 1 1 ⇔ x - 1 - 3 4 = y + 1 1 ⇔ ⇔ 1 x - 1 = - 3 4 y + 1 ⇔ x + 3 4 y - 1 4 = 0

The coefficients of the variables x and y give us the required coordinates of the normal vector. Thus, the normal vector of the line x = 1 - 3 4 · λ y = - 1 + λ has coordinates 1 , 3 4 .

Answer: 1 , 3 4 .

If you notice a mistake in the text, please highlight it and press Ctrl+Enter

The straight line together with the point are important elements of geometry, with the help of which many figures are built in space and on the plane. This article discusses in detail the parametric and its relationship with other types of equations for this geometric element.

Straight line and equations to describe it

A straight line in geometry is a collection of points that connect arbitrary two points in space by a segment with the smallest length. This segment is part of a straight line. Any other curves connecting two fixed points in space will have a large length, so they are not straight lines.

The picture above shows two black dots. The blue line connecting them is straight and the red line is curved. Obviously, the red line between the black dots is longer than the blue one.

There are several types of straight line equations that can be used to describe a straight line in three-dimensional space or in two-dimensional space. Below are the names of these equations:

• vector;
• parametric;
• in segments;
• symmetrical or canonical;
• general type.

In this article, we will consider the parametric equation of a straight line, but we will derive it from the vector one. We will also show the relationship between parametric and symmetric or canonical equations.

vector equation

It is clear that all the above types of equations for the considered geometric element are interconnected. Nevertheless, the vector equation is basic for all of them, since it directly follows from the definition of a straight line. Let us consider how it is introduced into geometry.

Suppose we are given a point in the space P(x 0 ; y 0 ; z 0). It is known that this point belongs to the line. How many lines can be drawn through it? Infinite set. Therefore, in order to be able to draw a single straight line, it is necessary to set the direction of the latter. The direction, as you know, is determined by the vector. Let's denote it v¯(a; b; c), where the symbols in brackets are its coordinates. For each point Q(x; y; z), which is on the line under consideration, we can write the equality:

(x; y; z) = (x 0 ; y 0 ; z 0) + α × (a; b; c)

Here the symbol α is a parameter that takes absolutely any real value (multiplying a vector by a number can only change its modulus or direction to the opposite). This equality is called the vector equation for a straight line in three-dimensional space. By changing the parameter α, we get all the points (x; y; z) that form this line.

The vector v¯(a; b; c) in the equation is called the direction vector. A straight line has no particular direction, and its length is infinite. These facts mean that any vector obtained from v¯ by multiplying by a real number will also be a guide for the line.

As for the point P(x 0; y 0; z 0), instead of it, an arbitrary point can be substituted into the equation, which lies on a straight line, and the latter will not change.

The figure above shows a straight line (blue line) that is defined in space through a direction vector (red line segment).

It is not difficult to obtain a similar equality for the two-dimensional case. Using similar reasoning, we arrive at the expression:

(x; y) = (x 0 ; y 0) + α × (a; b)

We see that it is completely the same as the previous one, only two coordinates are used instead of three to specify points and vectors.

Parametric equation

First, we obtain a parametric equation of a straight line in space. Above, when vector equality was written, it was already mentioned about the parameter that is present in it. To get a parametric equation, it is enough to expand the vector one. We get:

x = x 0 + α × a;

y = y0 + α × b;

z = z 0 + α × c

The set of these three linear equalities, each of which has one variable coordinate and parameter α, is usually called the parametric equation of a straight line in space. In fact, we have not done anything new, but simply explicitly recorded the meaning of the corresponding vector expression. We note only one point: the number α, although it is arbitrary, is the same for all three equalities. For example, if α \u003d -1.5 for the 1st equality, then its same value should be substituted into the second and third equalities when determining the coordinates of the point.

The parametric equation of a straight line on a plane is similar to that for the spatial case. It is written as:

x = x 0 + α × a;

y = y0 + α × b

Thus, in order to compose a parametric equation of a straight line, one should write down the vector equation for it in an explicit form.

Obtaining the canonical equation

As noted above, all equations defining a straight line in space and on a plane are obtained one from the other. Let us show how to obtain a canonical straight line from a parametric equation. For the spatial case we have:

x = x 0 + α × a;

y = y0 + α × b;

z = z 0 + α × c

Let's express the parameter in each equality:

α \u003d (x - x 0) / a;

α \u003d (y - y 0) / b;

α \u003d (z - z 0) / c

Since the left-hand sides are the same, then the right-hand sides of the equalities are also equal to each other:

(x - x 0) / a = (y - y 0) / b = (z - z 0) / c

This is the canonical equation for a straight line in space. The value of the denominator in each expression is the corresponding coordinate. The values ​​in the numerator that are subtracted from each variable are the coordinates of a point on that line.

The corresponding equation for the case on the plane takes the form:

(x - x 0) / a = (y - y 0) / b

Equation of a straight line through 2 points

It is known that two fixed points, both in the plane and in space, uniquely define a straight line. Assume that the following two points on the plane are given:

How to write the equation of a straight line through them? The first step is to define a direction vector. Its coordinates are as follows:

PQ¯(x 2 - x 1 ; y 2 ​​- y 1)

Now you can write the equation in any of the three forms that were discussed in the paragraphs above. For example, the parametric equation of a straight line takes the form:

x \u003d x 1 + α × (x 2 - x 1);

y \u003d y 1 + α × (y 2 - y 1)

In canonical form, you can rewrite it like this:

(x - x 1) / (x 2 - x 1) = (y - y 1) / (y 2 - y 1)

It can be seen that the canonical equation includes the coordinates of both points, and these points can be changed in the numerator. So, the last equation can be rewritten as follows:

(x - x 2) / (x 2 - x 1) = (y - y 2) / (y 2 - y 1)

All written expressions are called equations of a straight line through 2 points.

Three dot problem

The coordinates of the following three points are given:

It is necessary to determine whether these points lie on the same line or not.

This problem should be solved as follows: first, draw up an equation of a straight line for any two points, and then substitute the coordinates of the third one into it and check whether they satisfy the resulting equality.

We compose an equation in terms of M and N in parametric form. For this, we apply the formula obtained in the paragraph above, which we generalize to the three-dimensional case. We have:

x = 5 + α × (-3);

y = 3 + α × (-1);

z = -1 + α × 1

Now let's substitute the coordinates of the point K into these expressions and find the value of the alpha parameter that corresponds to them. We get:

1 = 5 + α × (-3) => α = 4/3;

1 = 3 + α × (-1) => α = 4;

5 = -1 + α × 1 => α = -4

We found out that all three equalities will be valid if each of them takes a different value of the parameter α. The latter fact contradicts the condition of the parametric equation of a straight line, in which α must be equal for all equations. This means that the point K does not belong to the line MN, which means that all three points do not lie on the same line.

The problem of parallel lines

Given two equations of lines in parametric form. They are presented below:

x = -1 + 5 × α;

x = 2 - 6 × λ;

y = 4 - 3.6 × λ

It is necessary to determine whether the lines are parallel. The easiest way to determine the parallelism of two lines is using the coordinates of the direction vectors. Referring to the general formula of the parametric equation in two-dimensional space, we get that the direction vectors of each straight line will have coordinates:

Two vectors are parallel if one of them can be obtained by multiplying the other by some number. We divide the coordinates of the vectors in pairs, we get:

It means that:

v 2 ¯ = -1.2 × v 1 ¯

The direction vectors v 2 ¯ and v 1 ¯ are parallel, which means that the lines in the problem statement are also parallel.

Let's check if they are not the same line. To do this, you need to substitute the coordinates of any point in the equation for another. Take the point (-1; 3), substitute it into the equation for the second straight line:

1 = 2 - 6 × λ => λ = 1/2;

3 \u003d 4 - 3.6 × λ => λ ≈ 0.28

That is, the lines are different.

The problem of perpendicularity of lines

Equations of two straight lines are given:

x = 2 + 6 × λ;

y = -2 - 4 × λ

Are these lines perpendicular?

Two lines will be perpendicular if the dot product of their direction vectors is zero. Let's write these vectors:

Let's find their scalar product:

(v 1 ¯ × v 2 ¯) = 2 × 6 + 3 × (-4) = 12 - 12 = 0

Thus, we found out that the considered lines are perpendicular. They are shown in the picture above.

Equating in the canonical equations of the straight line each of the fractions to some parameter t:

We obtain equations expressing the current coordinates of each point of the straight line through the parameter t.

thus, the parametric equations of the straight line have the form:

Equations of a straight line passing through two given points.

Let two points M 1 (x1,y1,z1) and M 2 (x2,y2,z2). The equations of a straight line passing through two given points are obtained in the same way as a similar equation on a plane. Therefore, we immediately give the form of this equation.

A straight line at the intersection of two planes. General equation of a straight line in space.

If we consider two non-parallel planes, then their intersection will be a straight line.

If the normal vectors and non-collinear.

Below, when considering examples, we will show a way to transform such straight line equations to canonical equations.

5.4 Angle between two straight lines. Condition of parallelism and perpendicularity of two lines.

An angle between two straight lines in space is any of the angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two lines be given by their canonical equations.

For the angle between two straight lines we will take the angle between the direction vectors.

And

The condition of perpendicularity of two straight lines is reduced to the condition of perpendicularity of their direction vectors and , that is, to the equality to zero of the scalar product: or in coordinate form: .

The condition of parallelism of two lines is reduced to the condition of parallelism of their direction vectors and

5.5 Mutual arrangement straight and plane.

Let the equations of the straight line be given:

and planes. The angle between the line and the plane will be any of the two adjacent angles formed by the line and its projection onto the plane (Figure 5.5).

Figure 5.5

If the line is perpendicular to the plane, the directing vector of the line and the normal vector to the plane are collinear. Thus, the condition of perpendicularity of a straight line and a plane is reduced to the condition of collinear vectors

In the case of parallelism of a straight line and a plane, their vectors indicated above are mutually perpendicular. Therefore, the condition of parallelism of a straight line and a plane is reduced to the condition of perpendicularity of the vectors; those. their dot product is zero or in coordinate form: .

Below are examples of solving problems related to the topic of Chapter 5.

Example 1:

Write an equation for a plane passing through point A (1,2,4) perpendicular to the straight line given by the equation:

Solution:

We use the equation of a plane passing through a given point perpendicular to a given vector.

A(x-x 0)+B(y-y 0)+C(z-z 0)=0

As a point, we take the point A (1,2,4), through which the plane passes by the condition.

Knowing the canonical equations of the line, we know the vector parallel to the line.

Due to the fact that, by the condition, the line is perpendicular to the desired plane, the direction vector can be taken as the normal vector of the plane.

Thus, we obtain the equation of the plane in the form:

2(x-1)+1(y-2)+4(z-4)=0

2x+y+4z-16=0

2x+y+4z-20=0

Example 2:

Find on the plane 4x-7y+5z-20=0 a point P for which OP makes equal angles with the coordinate axes.

Solution:

Let's make a schematic drawing. (Figure 5.6)

at

Figure 5.6

The empty point Р has coordinates . Since the vector makes the same angles with the coordinate axes, the direction cosines of this vector are equal to each other

Let's find the projections of the vector:

then the direction cosines of this vector are easily found.

From the equality of the direction cosines, the equality follows:

x p \u003d y p \u003d z p

since the point P lies on the plane, substituting the coordinates of this point into the equation of the plane turns it into an identity.

4x p -7x p +5x p -20=0

2x p \u003d 20

x p \u003d 10

Respectively: y r=10; z p=10.

Thus, the desired point P has coordinates P (10; 10; 10)

Example 3:

Given two points A (2, -1, -2) and B (8, -7.5). Find the equation of the plane passing through the point B, perpendicular to the segment AB.

Solution:

To solve the problem, we use the equation of a plane passing through a given point perpendicular to a given vector.

A(x-x 0)+B(y-y 0)+C(z-z 0)=0

As a point, we use point B (8, -7.5), and as a vector perpendicular to the plane, vector. Let's find the projections of the vector:

then we get the equation of the plane in the form:

6(x-8)-6(y+7)+7(z-5)=0

6x-48-6y-42+7z-35=0

6x-6y+7z-35=0

6x-6y+7z-125=0

Example 4:

Find the equation of a plane parallel to the OY axis and passing through the points K(1,-5,1) and M(3,2,-2).

Solution:

Since the plane is parallel to the OY axis, we will use the incomplete equation of the plane.

Ax+Cz+D=0

Due to the fact that the points K and M lie on the plane, we obtain two conditions.

Let us express from these conditions the coefficients A and C in terms of D.

We substitute the found coefficients into the incomplete equation of the plane:

since , then we reduce D:

Example 5:

Find the equation of a plane passing through three points M(7,6,7), K(5,10,5), R(-1,8,9)

Solution:

Let's use the equation of a plane passing through 3 given points.

substituting the coordinates points M, K, R as the first, second and third we get:

expand the determinant along the 1st line.

Example 6:

Find the equation of the plane passing through the points M 1 (8, -3,1); M 2 (4,7,2) and perpendicular to the plane 3x+5y-7z-21=0

Solution:

Let's make a schematic drawing (Figure 5.7)

Figure 5.7

We denote the given plane P 2 and the desired plane P 2. . From the equation given planeР 1 we determine the projections of the vector perpendicular to the plane Р 1.

The vector can be moved to the plane P 2 by means of parallel translation, since, according to the condition of the problem, the plane P 2 is perpendicular to the plane P 1, which means that the vector is parallel to the plane P 2.

Let's find the projections of the vector lying in the plane Р 2:

now we have two vectors and lying in the plane R 2 . Obviously, the vector equal to the vector product of the vectors and will be perpendicular to the plane P 2, since it is perpendicular to and, therefore, its normal vector to the plane P 2.

The vectors and are given by their projections, therefore:

Next, we use the equation of a plane passing through a given point perpendicular to the vector. As a point, you can take any of the points M 1 or M 2, for example M 1 (8, -3.1); As a normal vector to the plane Р 2 we take .

74(x-8)+25(y+3)+50(z-1)=0

3(x-8)+(y-3)+2(z-1)=0

3x-24+y+3+27-2=0

3x+y+2z-23=0

Example 7:

A straight line is defined by the intersection of two planes. Find the canonical equations of the line.

Solution:

We have an equation in the form:

Need to find a point x 0, y 0, z 0) through which the straight line and direction vector pass.

We choose one of the coordinates arbitrarily. For example, z=1, then we get a system of two equations with two unknowns:

Thus, we have found a point lying on the desired line (2,0,1).

As a directing vector of the desired straight line, we take the cross product of vectors and , which are normal vectors since , which means parallel to the desired line.

Thus, the direction vector of the straight line has projections . Using the equation of a straight line passing through a given point parallel to a given vector:

So the desired canonical equation has the form:

Example 8:

Find the coordinates of the point of intersection of a line and plane 2x+3y+3z-8=0

Solution:

Let us write the given equation of a straight line in a parametric form.

x=3t-2; y=-t+2; z=2t-1

each point of the straight line corresponds to a single value of the parameter t. To find the parameter t corresponding to the point of intersection of the line and the plane, we substitute the expression into the equation of the plane x, y, z via parameter t.

2(3t-2)+(-t+2)+3(2t-1)-8=0

6t-4-3t+6+6t-3-8=0

t=1

then the coordinates of the desired point

the desired intersection point has coordinates (1;1;1).

Example 9:

Find the equation of a plane passing through parallel lines.

Let's make a schematic drawing (Figure 5.9)

Figure 5.9

From the given equations of lines and we determine the projections of the directing vectors of these lines. We find the projections of the vector lying in the plane P, and take the points and from the canonical equations of the lines M 1 (1, -1,2) and M 2 (0,1, -2).

ANGLE BETWEEN PLANES

Let's consider two planes α 1 and α 2 given respectively by the equations:

Under corner between two planes we mean one of the dihedral angles formed by these planes. It is obvious that the angle between the normal vectors and the planes α 1 and α 2 is equal to one of the indicated adjacent dihedral angles or . That's why . Because And , That

.

Example. Determine the angle between planes x+2y-3z+4=0 and 2 x+3y+z+8=0.

Condition of parallelism of two planes.

Two planes α 1 and α 2 are parallel if and only if their normal vectors and are parallel, and hence .

So, two planes are parallel to each other if and only if the coefficients at the corresponding coordinates are proportional:

or

Condition of perpendicularity of planes.

It is clear that two planes are perpendicular if and only if their normal vectors are perpendicular, and therefore, or .

Thus, .

Examples.

DIRECT IN SPACE.

VECTOR EQUATION DIRECT.

PARAMETRIC EQUATIONS DIRECT

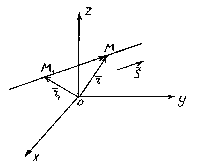
The position of a straight line in space is completely determined by specifying any of its fixed points M 1 and a vector parallel to this line.

A vector parallel to a straight line is called guiding the vector of this line.

So let the straight l passes through a point M 1 (x 1 , y 1 , z 1) lying on a straight line parallel to the vector .

Consider an arbitrary point M(x,y,z) on a straight line. It can be seen from the figure that .

The vectors and are collinear, so there is such a number t, what , where is the multiplier t can take any numeric value depending on the position of the point M on a straight line. Factor t is called a parameter. Denoting the radius vectors of points M 1 and M respectively, through and , we obtain . This equation is called vector straight line equation. It shows that each parameter value t corresponds to the radius vector of some point M lying on a straight line.

We write this equation in coordinate form. Notice, that , and from here

The resulting equations are called parametric straight line equations.

When changing the parameter t coordinates change x, y And z and dot M moves in a straight line.

CANONICAL EQUATIONS DIRECT

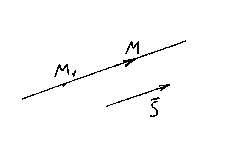
Let M 1 (x 1 , y 1 , z 1) - a point lying on a straight line l, And is its direction vector. Again, take an arbitrary point on a straight line M(x,y,z) and consider the vector .

It is clear that the vectors and are collinear, so their respective coordinates must be proportional, hence

– canonical straight line equations.

Remark 1. Note that the canonical equations of the line could be obtained from the parametric equations by eliminating the parameter t. Indeed, from the parametric equations we obtain or .

Example. Write the equation of a straight line in a parametric way.

Denote , hence x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Remark 2. Let the line be perpendicular to one of the coordinate axes, for example, the axis Ox. Then the direction vector of the line is perpendicular Ox, hence, m=0. Consequently, the parametric equations of the straight line take the form

Eliminating the parameter from the equations t, we obtain the equations of the straight line in the form

However, in this case too, we agree to formally write the canonical equations of the straight line in the form . Thus, if the denominator of one of the fractions is zero, then this means that the line is perpendicular to the corresponding coordinate axis.

Similarly, the canonical equations corresponds to a straight line perpendicular to the axes Ox And Oy or parallel axis Oz.

Examples.

GENERAL EQUATIONS A DIRECT LINE AS A LINE OF INTERCEPTION OF TWO PLANES

Through each straight line in space passes an infinite number of planes. Any two of them, intersecting, define it in space. Therefore, the equations of any two such planes, considered together, are the equations of this line.

In general, any two non-parallel planes given by the general equations

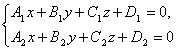
determine their line of intersection. These equations are called general equations straight.

Examples.

Construct a straight line given by equations

To construct a line, it is enough to find any two of its points. The easiest way is to choose the points of intersection of the line with the coordinate planes. For example, the point of intersection with the plane xOy we obtain from the equations of a straight line, assuming z= 0:

Solving this system, we find the point M 1 (1;2;0).

Similarly, assuming y= 0, we get the point of intersection of the line with the plane xOz:

From the general equations of a straight line, one can proceed to its canonical or parametric equations. To do this, you need to find some point M 1 on the line and the direction vector of the line.

Point coordinates M 1 we obtain from this system of equations, giving one of the coordinates an arbitrary value. To find the direction vector, note that this vector must be perpendicular to both normal vectors And . Therefore, for the direction vector of the straight line l you can take vector product normal vectors:

.

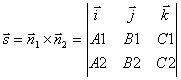Example. Lead general equations straight to the canonical form.

Find a point on a straight line. To do this, we choose arbitrarily one of the coordinates, for example, y= 0 and solve the system of equations:

The normal vectors of the planes defining the line have coordinates Therefore, the direction vector will be straight

. Hence, l: .

ANGLE BETWEEN RIGHTS

corner between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two straight lines be given in space:

Obviously, the angle φ between the lines can be taken as the angle between their direction vectors and . Since , then according to the formula for the cosine of the angle between the vectors we get