Какво представляват функционалните нули? Отговорът е много прост - това е математически термин, който означава областта на дефиниране на дадена функция, в която нейната стойност е нула. Функционалните нули също се наричат. Най-лесният начин да обясните какво представляват функционалните нули е с няколко прости примера.

Примери

Нека разгледаме простото уравнение y=x+3. Тъй като нулата на функция е стойността на аргумента, при който y е придобил нулева стойност, ние заместваме 0 в лявата страна на уравнението:

В този случай -3 е желаната нула. За дадена функция има само един корен на уравнението, но това не винаги е така.

Нека да разгледаме друг пример:

Нека заместим 0 в лявата страна на уравнението, както в предишния пример:

Очевидно в този случай ще има две нули на функцията: x=3 и x=-3. Ако уравнението имаше аргумент от трета степен, щеше да има три нули. Може да се направи просто заключение, че броят на корените на полинома съответства на максималната степен на аргумента в уравнението. Много функции обаче, например y = x 3, на пръв поглед противоречат на това твърдение. Логиката и здравият разум диктуват, че тази функция има само една нула - в точката x=0. Но всъщност има три корена, те просто всички съвпадат. Ако решите уравнението в сложна форма, това става очевидно. x=0 в този случай, корен, чиято кратност е 3. В предишния пример нулите не съвпадаха, следователно имаха кратност 1.

Алгоритъм за определяне

От представените примери можете да видите как се определят нулите на функция. Алгоритъмът е винаги един и същ:

1. Напишете функция.
2. Заместете y или f(x)=0.
3. Решете полученото уравнение.

Трудността на последната точка зависи от степента на аргумента на уравнението. Когато решавате уравнения с високи степени, особено важно е да запомните, че броят на корените на уравнението е равен на максималната степен на аргумента. Това е особено вярно за тригонометричните уравнения, където разделянето на двете страни на синус или косинус води до загуба на корени.

Уравнения с произволна степен са най-лесни за решаване с помощта на метода на Хорнер, който е разработен специално за намиране на нулите на произволен полином.

Стойността на нулите на функциите може да бъде отрицателна или положителна, реална или в комплексната равнина, единична или множествена. Или може да няма корени на уравнението. Например функцията y=8 няма да придобие нулева стойност за нито едно x, защото не зависи от тази променлива.

Уравнението y=x 2 -16 има два корена и двата лежат в комплексната равнина: x 1 =4i, x 2 =-4i.

Често допускани грешки

Често срещана грешка, допускана от ученици, които все още не са разбрали напълно какво представляват нулите на функцията, е замяната на аргумента (x) с нула, а не със стойността (y) на функцията. Те уверено заместват x=0 в уравнението и въз основа на това намират y. Но това е грешен подход.

Друга грешка, както вече беше споменато, е намаляването със синус или косинус в тригонометрично уравнение, поради което се губят една или повече нули от функцията. Това не означава, че нищо не може да бъде намалено в такива уравнения, но при по-нататъшни изчисления е необходимо да се вземат предвид тези „загубени“ фактори.

Графично представяне

Можете да разберете какви са нулите на дадена функция с помощта на математически програми като Maple. В него можете да изградите графика, като посочите желания брой точки и желания мащаб. Точките, в които графиката пресича оста OX, са желаните нули. Това е един от най-бързите начини за намиране на корените на полином, особено ако редът му е по-висок от трети. Така че, ако има нужда от редовно извършване на математически изчисления, намиране на корените на полиноми с произволни степени, изграждане на графики, Maple или подобна програма ще бъде просто незаменима за извършване и проверка на изчисления.

2. Да намерим нулите на функцията.

f(x) при x .

Отговор f(x) при x .

2) x 2 >-4x-5;

x 2 +4x +5>0;

Нека f(x)=x 2 +4x +5 тогава Нека намерим такова x, за което f(x)>0,

D=-4 Без нули.

4. Системи от неравенства. Неравенства и системи от неравенства с две променливи

1) Множеството от решения на система от неравенства е пресечната точка на множествата от решения на неравенствата, включени в нея.

2) Множеството от решения на неравенството f(x;y)>0 може да се изобрази графично върху координатната равнина. Обикновено правата, определена от уравнението f(x;y) = 0, разделя равнината на 2 части, едната от които е решението на неравенството. За да определите коя част, трябва да замените координатите на произволна точка M(x0;y0), която не лежи на правата f(x;y)=0 в неравенството. Ако f(x0;y0) > 0, тогава решението на неравенството е частта от равнината, съдържаща точката M0. ако f(x0;y0)<0, то другая часть плоскости.

3) Множеството от решения на система от неравенства е пресечната точка на множествата от решения на неравенствата, включени в нея. Нека например ни е дадена система от неравенства:

.

За първото неравенство наборът от решения е окръжност с радиус 2 и център в началото, а за второто е полуравнина, разположена над правата линия 2x+3y=0. Множеството от решения на тази система е пресечната точка на тези множества, т.е. полукръг.

4) Пример. Решете системата от неравенства:

Решението на първото неравенство е множеството , второто е множеството (2;7) и третото е множеството .

Пресечната точка на тези множества е интервалът (2;3], който е множеството от решения на системата от неравенства.

5. Решаване на рационални неравенства по интервалния метод

Методът на интервалите се основава на следното свойство на бинома (x-a): точката x = α разделя числовата ос на две части - вдясно от точката α биномът (x-α)>0, а към вляво от точката α (x-α)<0.

Нека е необходимо да се реши неравенството (x-α 1)(x-α 2)...(x-α n)>0, където α 1, α 2 ...α n-1, α n са фиксирани числа, сред които няма равни и такива, че α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 с помощта на интервалния метод се процедира по следния начин: числата α 1, α 2 ...α n-1, α n се нанасят върху числената ос; в интервала вдясно от най-големия от тях, т.е. числа α n, поставете знак плюс, в интервала след него отдясно наляво поставете знак минус, след това знак плюс, след това знак минус и т.н. Тогава множеството от всички решения на неравенството (x-α 1)(x-α 2)...(x-α n)>0 ще бъде обединението на всички интервали, в които е поставен знакът плюс, и множеството на решенията на неравенството (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) Решаване на рационални неравенства (т.е. неравенства от вида P(x) Q(x) където са полиноми) се основава на следното свойство на непрекъсната функция: ако непрекъсната функция изчезва в точки x1 и x2 (x1; x2) и няма други корени между тези точки, тогава в интервали (x1; x2) функцията запазва знака си.

Следователно, за да намерите интервали с постоянен знак на функцията y=f(x) на числовата ос, маркирайте всички точки, в които функцията f(x) изчезва или претърпява прекъсване. Тези точки разделят числовата права на няколко интервала, във всеки от които функцията f(x) е непрекъсната и не се занулява, т.е. запазва знака. За да се определи този знак, достатъчно е да се намери знакът на функцията във всяка точка от разглеждания интервал на числовата линия.

2) Да се ​​определят интервали с постоянен знак на рационална функция, т.е. За да решим рационално неравенство, отбелязваме на числовата ос корените на числителя и корените на знаменателя, които също са корените и точките на прекъсване на рационалната функция.

Решаване на неравенства по интервалния метод

3. < 20.

Решение. Диапазонът на допустимите стойности се определя от системата от неравенства:

За функцията f(x) = – 20. Намерете f(x):

откъдето x = 29 и x = 13.

f(30) = – 20 = 0,3 > 0,

f(5) = – 1 – 20 = – 10< 0.

Отговор: . Основни методи за решаване на рационални уравнения. 1) Най-простият: решава се чрез обичайните опростявания - редуциране до общ знаменател, редуциране на подобни членове и т.н. Квадратните уравнения ax2 + bx + c = 0 се решават чрез...

X се променя на интервала (0,1] и намалява на интервала .

Виждаме това добавяне нкъм аргумента х, не се променя

стойност на функцията. Най-малкото различно от нула число

от не , така че това е периодът sin 2 х .

Функционални нули. Извиква се стойността на аргумента, при която функцията е равна на 0 нула ( root) функция. Една функция може да има няколко нули. Например функцията г = х (х + 1) (х- 3) има три нули: х = 0, х = — 1, х= 3. Геометрично нулева функция – това е абсцисата на пресечната точка на графиката на функцията с оста х .

Фигура 7 показва графика на функция с нули: х = а , х = bИ х = ° С .

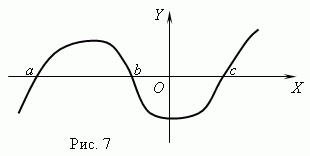
Асимптота. Ако графиката на функция се приближава неограничено до определена права, докато се отдалечава от началото, тогава тази права се нарича асимптота.

Тема 6. „Интервален метод“.

Ако f (x) f (x 0) за x x 0, тогава се извиква функцията f (x). непрекъснато в точка x 0.

Ако една функция е непрекъсната във всяка точка от някакъв интервал I, тогава тя се нарича непрекъснато на интервала I (интервалът I се нарича интервал на непрекъснатост на функцията). Графиката на функция в този интервал е непрекъсната линия, която според тях може да бъде „начертана, без да се вдига моливът от хартията“.

Свойство на непрекъснатите функции.

Ако на интервала (a ; b) функцията f е непрекъсната и не се нулира, то тя запазва постоянен знак на този интервал.

Методът за решаване на неравенства с една променлива, интервалният метод, се основава на това свойство. Нека функцията f(x) е непрекъсната в интервала I и се нулира в краен брой точки в този интервал. По свойството на непрекъснатите функции тези точки разделят I на интервали, във всеки от които непрекъснатата функция f(x) c поддържа постоянен знак. За да се определи този знак, е достатъчно да се изчисли стойността на функцията f(x) във всяка точка от всеки такъв интервал. Въз основа на това получаваме следния алгоритъм за решаване на неравенства по интервалния метод.

Интервален метод за неравенства на вида

Намерете областта на дефиниция на функцията f(x) ;

Намерете нулите на функцията f(x) ;

Начертайте дефиниционната област и нулите на функцията върху числовата ос. Нулите на функция разделят нейната област на дефиниция на интервали, във всеки от които функцията запазва постоянен знак;

Намерете знаците на функцията в получените интервали, като изчислите стойността на функцията във всяка точка от всеки интервал;

Запишете отговора.

Интервален метод. Средно ниво.

Искате ли да изпробвате силата си и да разберете резултата от това колко сте готови за Единния държавен изпит или Единния държавен изпит?

Линейна функция

Функция на формата се нарича линейна. Нека вземем функция като пример. Той е положителен при 3″> и отрицателен при. Точката е нулата на функцията (). Нека да покажем знаците на тази функция върху числовата ос:

Казваме, че „функцията променя знака при преминаване през точката“.

Вижда се, че знаците на функцията съответстват на позицията на графиката на функцията: ако графиката е над оста, знакът е “ ”, ако под нея е “ ”.

Ако обобщим полученото правило до произволна линейна функция, получаваме следния алгоритъм:

Намиране на нулата на функцията;

Маркираме го на числовата ос;

Определяме знака на функцията от противоположните страни на нулата.

Квадратична функция

Надявам се, че си спомняте как се решават квадратни неравенства? Ако не, прочетете темата „Квадратни неравенства“. Нека ви напомня за общия вид на квадратична функция: .

Сега нека си спомним какви знаци приема квадратичната функция. Графиката му е парабола и функцията приема знака " " за тези, в които параболата е над оста, и " " - ако параболата е под оста:

Ако функцията има нули (стойности, при които), параболата пресича оста в две точки - корените на съответното квадратно уравнение. Така оста е разделена на три интервала и знаците на функцията се променят последователно при преминаване през всеки корен.

Възможно ли е по някакъв начин да се определят знаците, без всеки път да се рисува парабола?

Спомнете си, че квадратен трином може да бъде факторизиран:

Нека маркираме корените на оста:

Спомняме си, че знакът на функция може да се промени само при преминаване през корена. Нека използваме този факт: за всеки от трите интервала, на които оста е разделена с корени, е достатъчно да определим знака на функцията само в една произволно избрана точка: в останалите точки от интервала знакът ще бъде същият .

В нашия пример: при 3″> и двата израза в скоби са положителни (заместете, например: 0″>). Поставяме знак " " на оста:

Е, когато (заместител, например), и двете скоби са отрицателни, което означава, че продуктът е положителен:

Това е, което е интервален метод: знаейки знаците на факторите на всеки интервал, ние определяме знака на целия продукт.

Нека разгледаме и случаите, когато функцията няма нули или има само една.

Ако ги няма, значи няма корени. Това означава, че няма да има „преминаване през корена“. Това означава, че функцията приема само един знак на цялата числова ос. Може лесно да се определи чрез заместването му във функция.

Ако има само един корен, параболата докосва оста, така че знакът на функцията не се променя при преминаване през корена. Какво правило можем да измислим за такива ситуации?

Ако факторизирате такава функция, получавате два еднакви фактора:

И всеки израз на квадрат е неотрицателен! Следователно знакът на функцията не се променя. В такива случаи ще подчертаем корена, при преминаване през който знакът не се променя, като го оградим с квадрат:

Ще наречем такъв корен кратни.

Интервален метод в неравенствата

Сега всяко квадратно неравенство може да бъде решено без да се чертае парабола. Достатъчно е просто да поставите знаците на квадратичната функция върху оста и да изберете интервали в зависимост от знака на неравенството. Например:

Нека измерим корените на оста и да поставим знаците:

Нуждаем се от частта от оста със знака " "; тъй като неравенството не е строго, самите корени също са включени в решението:

Сега разгледайте рационално неравенство - неравенство, двете страни на което са рационални изрази (вижте „Рационални уравнения“).

Пример:

Всички фактори с изключение на един са „линейни“ тук, тоест съдържат променлива само на първа степен. Такива линейни множители ни трябват, за да приложим интервалния метод - знакът се променя при преминаване през техните корени. Но множителят изобщо няма корени. Това означава, че то винаги е положително (проверете това сами) и следователно не влияе върху знака на цялото неравенство. Това означава, че можем да разделим лявата и дясната страна на неравенството с него и по този начин да се отървем от него:

Сега всичко е същото, както беше с квадратните неравенства: определяме в кои точки всеки от факторите става нула, отбелязваме тези точки на оста и подреждаме знаците. Искам да обърна внимание на един много важен факт:

В случай на четно число правим същото като преди: ограждаме точката с квадрат и не променяме знака при преминаване през корена. Но в случай на нечетно число това правило не важи: знакът все пак ще се промени, когато преминава през корена. Следователно не правим нищо допълнително с такъв корен, сякаш не е кратно. Горните правила се прилагат за всички четни и нечетни степени.

Какво да напишем в отговора?

Ако редуването на знаците е нарушено, трябва да сте много внимателни, защото ако неравенството не е строго, отговорът трябва да включва всички защриховани точки. Но някои от тях често стоят отделно, тоест не са включени в сенчестата зона. В този случай ги добавяме към отговора като изолирани точки (във фигурни скоби):

Примери (решете сами):

Отговори:

1. Ако сред факторите е прост, той е корен, защото може да бъде представен като.
   .

В който приема стойност нула. Например за функция, дадена от формулата

Е нула, защото

.

Нулите на функция също се наричат корени на функцията.

Концепцията за нули на функция може да се разглежда за всякакви функции, чийто диапазон от стойности съдържа нула или нулевия елемент на съответната алгебрична структура.

За функция на реална променлива нулите са стойностите, при които графиката на функцията пресича оста x.

Намирането на нулите на функция често изисква използването на числени методи (например метод на Нютон, градиентни методи).

Един от нерешените математически проблеми е намирането на нулите на дзета функцията на Риман.

Корен на полином

Вижте също

Литература

Фондация Уикимедия. 2010 г.

Вижте какво е „Функция нула“ в други речници:

Точката, в която дадена функция f(z) изчезва; по този начин, N. f. f (z) е същото като корените на уравнението f (z) = 0. Например точките 0, π, π, 2π, 2π,... са нули на функцията sinz. Нули на аналитична функция (Вижте Аналитични... ...

Нулева функция, нулева функция... Правописен речник-справочник

Този термин има други значения, вижте Нула. Съдържанието на тази статия трябва да бъде преместено в статията „Нулева функция“. Можете да помогнете на проекта, като комбинирате статии. Ако е необходимо да се обсъди осъществимостта на сливането, заменете това ... Wikipedia

Или C string (от името на езика C) или ASCIZ string (от името на директивата на асемблера.asciz) метод за представяне на низове в езиците за програмиране, в който вместо въвеждане на специален тип низ, масив от знаци се използва, а в края ... ... Wikipedia

В квантовата теория на полето приетото (на жаргон) наименование за свойството за изчезване на коефициента на пренормиране на константата на свързване е където g0 е константата на голото свързване от лагранжиана на взаимодействието, физически. константа на свързване, облечена като взаимодействие. Равенство Z... Физическа енциклопедия

Нулева мутация n-алел- Нулева мутация, n. алел * нулева мутация, n. алел * нулева мутация или n. алелен или тих а. мутация, водеща до пълна загуба на функция в ДНК последователността, в която се е появила... Генетика. енциклопедичен речник

Твърдението в теорията на вероятностите, че всяко събитие (така нареченото остатъчно събитие), появата на което се определя само от произволно отдалечени елементи на поредица от независими случайни събития или случайни променливи, има... ... Математическа енциклопедия

1) Число, което има свойството, че всяко (реално или комплексно) число не се променя, когато се добави към него. Означава се със символа 0. Произведението на всяко число от N. е равно на N.: Ако произведението на две числа е равно на N., тогава един от факторите ... Математическа енциклопедия

Функции, дефинирани от връзки между независими променливи, които не са разрешени спрямо последните; тези отношения са един от начините за специфициране на функция. Например връзката x2 + y2 1 = 0 определя N.f. ... Велика съветска енциклопедия