What are function zeros? The answer is quite simple - this is a mathematical term, which means the domain of definition of a given function, in which its value is zero. Function zeros are also called. The easiest way to explain what function zeros are is with a few simple examples.

Examples

Let's consider the simple equation y=x+3. Since the zero of a function is the value of the argument at which y acquired a zero value, we substitute 0 on the left side of the equation:

In this case, -3 is the desired zero. For a given function there is only one root of the equation, but this is not always the case.

Let's look at another example:

Let's substitute 0 on the left side of the equation, as in the previous example:

Obviously, in this case there will be two zeros of the function: x=3 and x=-3. If the equation had a third-degree argument, there would be three zeros. A simple conclusion can be drawn that the number of roots of the polynomial corresponds to the maximum degree of the argument in the equation. However, many functions, for example y = x 3, at first glance contradict this statement. Logic and common sense dictate that this function has only one zero - at the point x=0. But in fact there are three roots, they just all coincide. If you solve the equation in complex form, this becomes obvious. x=0 in this case, a root whose multiplicity is 3. In the previous example, the zeros did not coincide, therefore they had a multiplicity of 1.

Determination algorithm

From the presented examples you can see how to determine the zeros of a function. The algorithm is always the same:

1. Write a function.
2. Substitute y or f(x)=0.
3. Solve the resulting equation.

The difficulty of the last point depends on the degree of the argument of the equation. When solving equations of high degrees, it is especially important to remember that the number of roots of the equation is equal to the maximum degree of the argument. This is especially true for trigonometric equations, where dividing both sides by sine or cosine leads to the loss of roots.

Equations of arbitrary degree are easiest to solve using Horner's method, which was developed specifically for finding the zeros of an arbitrary polynomial.

The value of zeros of functions can be either negative or positive, real or in the complex plane, singular or multiple. Or there may be no roots to the equation. For example, the function y=8 will not acquire a zero value for any x, because it does not depend on this variable.

The equation y=x 2 -16 has two roots, and both lie in the complex plane: x 1 =4i, x 2 =-4i.

Common mistakes

A common mistake made by schoolchildren who have not yet fully understood what zeros of a function are is replacing the argument (x) with zero, rather than the value (y) of the function. They confidently substitute x=0 into the equation and, based on this, find y. But this is the wrong approach.

Another mistake, as already mentioned, is reduction by sine or cosine in a trigonometric equation, which is why one or more zeros of the function are lost. This does not mean that nothing can be reduced in such equations, but in further calculations it is necessary to take into account these “lost” factors.

Graphical representation

You can understand what the zeros of a function are using mathematical programs such as Maple. You can build a graph in it by specifying the desired number of points and the desired scale. Those points at which the graph intersects the OX axis are the desired zeros. This is one of the fastest ways to find the roots of a polynomial, especially if its order is higher than third. So if there is a need to regularly perform mathematical calculations, find the roots of polynomials of arbitrary degrees, build graphs, Maple or a similar program will be simply indispensable for carrying out and checking calculations.

2. Let's find the zeros of the function.

f(x) at x .

Answer f(x) at x .

2) x 2 >-4x-5;

x 2 +4x +5>0;

Let f(x)=x 2 +4x +5 then Let us find such x for which f(x)>0,

D=-4 No zeros.

4. Systems of inequalities. Inequalities and systems of inequalities with two variables

1) The set of solutions to a system of inequalities is the intersection of the sets of solutions to the inequalities included in it.

2) The set of solutions to the inequality f(x;y)>0 can be graphically depicted on the coordinate plane. Typically, the line defined by the equation f(x;y) = 0 divides the plane into 2 parts, one of which is the solution to the inequality. To determine which part, you need to substitute the coordinates of an arbitrary point M(x0;y0) that does not lie on the line f(x;y)=0 into the inequality. If f(x0;y0) > 0, then the solution to the inequality is the part of the plane containing the point M0. if f(x0;y0)<0, то другая часть плоскости.

3) The set of solutions to a system of inequalities is the intersection of the sets of solutions to the inequalities included in it. Let, for example, be given a system of inequalities:

.

For the first inequality, the set of solutions is a circle of radius 2 and centered at the origin, and for the second, it is a half-plane located above the straight line 2x+3y=0. The set of solutions of this system is the intersection of these sets, i.e. semicircle.

4) Example. Solve the system of inequalities:

The solution to the 1st inequality is the set , the 2nd is the set (2;7) and the third is the set .

The intersection of these sets is the interval (2;3], which is the set of solutions to the system of inequalities.

5. Solving rational inequalities using the interval method

The method of intervals is based on the following property of the binomial (x-a): the point x = α divides the number axis into two parts - to the right of the point α the binomial (x-α)>0, and to the left of the point α (x-α)<0.

Let it be necessary to solve the inequality (x-α 1)(x-α 2)...(x-α n)>0, where α 1, α 2 ...α n-1, α n are fixed numbers, among which there are no equals, and such that α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 using the interval method proceed as follows: the numbers α 1, α 2 ...α n-1, α n are plotted on the numerical axis; in the interval to the right of the largest of them, i.e. numbers α n, put a plus sign, in the interval following it from right to left put a minus sign, then a plus sign, then a minus sign, etc. Then the set of all solutions to the inequality (x-α 1)(x‑α 2)...(x-α n)>0 will be the union of all intervals in which the plus sign is placed, and the set of solutions to the inequality (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) Solving rational inequalities (i.e. inequalities of the form P(x) Q(x) where are polynomials) is based on the following property of a continuous function: if a continuous function vanishes at points x1 and x2 (x1; x2) and has no other roots between these points, then in the intervals (x1; x2) the function retains its sign.

Therefore, to find intervals of constant sign of the function y=f(x) on the number line, mark all the points at which the function f(x) vanishes or suffers a discontinuity. These points divide the number line into several intervals, inside each of which the function f(x) is continuous and does not vanish, i.e. saves the sign. To determine this sign, it is enough to find the sign of the function at any point of the considered interval of the number line.

2) To determine intervals of constant sign of a rational function, i.e. To solve a rational inequality, we mark on the number line the roots of the numerator and the roots of the denominator, which are also the roots and breakpoints of the rational function.

Solving inequalities using the interval method

3. < 20.

Solution. The range of acceptable values ​​is determined by the system of inequalities:

For the function f(x) = – 20. Find f(x):

whence x = 29 and x = 13.

f(30) = – 20 = 0.3 > 0,

f(5) = – 1 – 20 = – 10< 0.

Answer: . Basic methods for solving rational equations. 1) The simplest: solved by the usual simplifications - reduction to a common denominator, reduction of similar terms, and so on. Quadratic equations ax2 + bx + c = 0 are solved by...

X changes on the interval (0,1], and decreases on the interval .

We see that adding n to the argument x, does not change

function value. Smallest non-zero number

from n is , so this is the period sin 2 x .

Function zeros. The argument value at which the function is equal to 0 is called zero ( root) function. A function may have multiple zeros. For example, the function y = x (x + 1) (x- 3) has three zeros: x = 0, x = — 1, x= 3. Geometrically null function – this is the abscissa of the point of intersection of the function graph with the axis X .

Figure 7 shows a graph of a function with zeros: x = a , x = b And x = c .

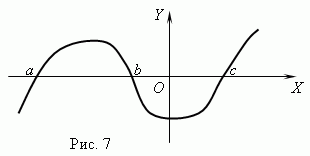
Asymptote. If the graph of a function indefinitely approaches a certain line as it moves away from the origin, then this line is called asymptote.

Topic 6. “Interval method.”

If f (x) f (x 0) for x x 0, then the function f (x) is called continuous at point x 0.

If a function is continuous at every point of some interval I, then it is called continuous on the interval I (the interval I is called continuity interval of the function). The graph of a function on this interval is a continuous line, which they say can be “drawn without lifting the pencil from the paper.”

Property of continuous functions.

If on the interval (a ; b) the function f is continuous and does not vanish, then it retains a constant sign on this interval.

A method for solving inequalities with one variable, the interval method, is based on this property. Let the function f(x) be continuous on the interval I and vanish at a finite number of points in this interval. By the property of continuous functions, these points divide I into intervals, in each of which the continuous function f(x) c maintains a constant sign. To determine this sign, it is enough to calculate the value of the function f(x) at any one point from each such interval. Based on this, we obtain the following algorithm for solving inequalities using the interval method.

Interval method for inequalities of the form

Find the domain of definition of the function f(x) ;

Find the zeros of the function f(x) ;

Plot the domain of definition and zeros of the function on the number line. The zeros of a function divide its domain of definition into intervals, in each of which the function retains a constant sign;

Find the signs of the function in the resulting intervals by calculating the value of the function at any one point from each interval;

Write down the answer.

Interval method. Average level.

Do you want to test your strength and find out the result of how ready you are for the Unified State Exam or Unified State Exam?

Linear function

A function of the form is called linear. Let's take a function as an example. It is positive at 3″> and negative at. The dot is the zero of the function (). Let's show the signs of this function on the number axis:

We say that “the function changes sign when passing through the point”.

It can be seen that the signs of the function correspond to the position of the function graph: if the graph is above the axis, the sign is “ ”, if below it is “ ”.

If we generalize the resulting rule to an arbitrary linear function, we obtain the following algorithm:

Finding the zero of the function;

We mark it on the number axis;

We determine the sign of the function on opposite sides of zero.

Quadratic function

I hope you remember how to solve quadratic inequalities? If not, read the topic “Quadratic Inequalities.” Let me remind you of the general form of a quadratic function: .

Now let's remember what signs the quadratic function takes. Its graph is a parabola, and the function takes the sign " " for those in which the parabola is above the axis, and " " - if the parabola is below the axis:

If a function has zeros (values ​​at which), the parabola intersects the axis at two points - the roots of the corresponding quadratic equation. Thus, the axis is divided into three intervals, and the signs of the function alternately change when passing through each root.

Is it possible to somehow determine the signs without drawing a parabola every time?

Recall that a square trinomial can be factorized:

Let's mark the roots on the axis:

We remember that the sign of a function can only change when passing through the root. Let's use this fact: for each of the three intervals into which the axis is divided by roots, it is enough to determine the sign of the function at only one arbitrarily chosen point: at the remaining points of the interval the sign will be the same.

In our example: at 3″> both expressions in brackets are positive (substitute, for example: 0″>). We put a “ ” sign on the axis:

Well, when (substitute, for example), both brackets are negative, which means the product is positive:

That's what it is interval method: knowing the signs of the factors on each interval, we determine the sign of the entire product.

Let's also consider cases when the function has no zeros, or only one.

If they are not there, then there are no roots. This means that there will be no “passing through the root”. This means that the function takes only one sign on the entire number line. It can be easily determined by substituting it into a function.

If there is only one root, the parabola touches the axis, so the sign of the function does not change when passing through the root. What rule can we come up with for such situations?

If you factor such a function, you get two identical factors:

And any squared expression is non-negative! Therefore, the sign of the function does not change. In such cases, we will highlight the root, when passing through which the sign does not change, by circling it with a square:

We will call such a root multiples.

Interval method in inequalities

Now any quadratic inequality can be solved without drawing a parabola. It is enough just to place the signs of the quadratic function on the axis and select intervals depending on the sign of the inequality. For example:

Let's measure the roots on the axis and place the signs:

We need the part of the axis with the " " sign; since the inequality is not strict, the roots themselves are also included in the solution:

Now consider a rational inequality - an inequality, both sides of which are rational expressions (see “Rational Equations”).

Example:

All factors except one are “linear” here, that is, they contain a variable only to the first power. We need such linear factors to apply the interval method - the sign changes when passing through their roots. But the multiplier has no roots at all. This means that it is always positive (check this for yourself), and therefore does not affect the sign of the entire inequality. This means that we can divide the left and right sides of the inequality by it, and thus get rid of it:

Now everything is the same as it was with quadratic inequalities: we determine at what points each of the factors becomes zero, mark these points on the axis and arrange the signs. I would like to draw your attention to a very important fact:

In the case of an even number, we do the same as before: we circle the point with a square and do not change the sign when passing through the root. But in the case of an odd number, this rule does not apply: the sign will still change when passing through the root. Therefore, we do not do anything additional with such a root, as if it were not a multiple. The above rules apply to all even and odd powers.

What should we write in the answer?

If the alternation of signs is violated, you need to be very careful, because if the inequality is not strict, the answer should include all shaded points. But some of them often stand apart, that is, they are not included in the shaded area. In this case, we add them to the answer as isolated points (in curly braces):

Examples (decide for yourself):

Answers:

1. If among the factors it is simple, it is a root, because it can be represented as.
   .

In which it takes the value zero. For example, for a function given by the formula

Is zero because

.

The zeros of a function are also called roots of the function.

The concept of zeros of a function can be considered for any functions whose range of values ​​contains zero or the zero element of the corresponding algebraic structure.

For a function of a real variable, zeros are the values ​​at which the graph of the function intersects the x-axis.

Finding the zeros of a function often requires the use of numerical methods (for example, Newton's method, gradient methods).

One of the unsolved mathematical problems is finding the zeros of the Riemann zeta function.

Root of a polynomial

see also

Literature

Wikimedia Foundation. 2010.

See what “Function Zero” is in other dictionaries:

The point where a given function f(z) vanishes; thus, N. f. f (z) is the same as the roots of the equation f (z) = 0. For example, the points 0, π, π, 2π, 2π,... are zeros of the function sinz. Zeros of an analytical function (See Analytical... ...

Zero function, zero function... Spelling dictionary-reference book

This term has other meanings, see Zero. The contents of this article should be moved to the "Function Null" article. You can help the project by combining articles. If it is necessary to discuss the feasibility of merging, replace this ... Wikipedia

Or C string (from the name of the C language) or ASCIZ string (from the name of the assembler directive.asciz) a method of representing strings in programming languages, in which instead of introducing a special string type, an array of characters is used, and at the end ... ... Wikipedia

In quantum field theory, the accepted (jargon) name for the property of vanishing the renormalization factor of the coupling constant is where g0 is the bare coupling constant from the interaction Lagrangian, physical. coupling constant dressed up as interaction. Equality Z... Physical encyclopedia

Null mutation n-allele- Null mutation, n. allele * null mutation, n. allele * null mutation or n. allel or silent a. a mutation leading to complete loss of function in the DNA sequence in which it occurred... Genetics. encyclopedic Dictionary

The statement in probability theory that any event (the so-called residual event), the occurrence of which is determined only by arbitrarily distant elements of a sequence of independent random events or random variables, has... ... Mathematical Encyclopedia

1) A number that has the property that any (real or complex) number does not change when added to it. Denoted by the symbol 0. The product of any number by N. is equal to N.: If the product of two numbers is equal to N., then one of the factors ... Mathematical Encyclopedia

Functions defined by relationships between independent variables that are not resolved relative to the latter; these relations are one of the ways to specify a function. For example, the relation x2 + y2 1 = 0 defines the N.f. ... Great Soviet Encyclopedia