Τι είναι τα μηδενικά συναρτήσεων; Η απάντηση είναι αρκετά απλή - αυτός είναι ένας μαθηματικός όρος, που σημαίνει το πεδίο ορισμού μιας δεδομένης συνάρτησης, στην οποία η τιμή της είναι μηδέν. Οι συναρτήσεις μηδενικά ονομάζονται επίσης. Ο ευκολότερος τρόπος για να εξηγήσετε τι είναι η συνάρτηση μηδενικά είναι με μερικά απλά παραδείγματα.

Παραδείγματα

Ας εξετάσουμε την απλή εξίσωση y=x+3. Δεδομένου ότι το μηδέν μιας συνάρτησης είναι η τιμή του ορίσματος στο οποίο το y απέκτησε μηδενική τιμή, αντικαθιστούμε το 0 στην αριστερή πλευρά της εξίσωσης:

Σε αυτή την περίπτωση, -3 είναι το επιθυμητό μηδέν. Για μια δεδομένη συνάρτηση υπάρχει μόνο μία ρίζα της εξίσωσης, αλλά αυτό δεν συμβαίνει πάντα.

Ας δούμε ένα άλλο παράδειγμα:

Ας αντικαταστήσουμε το 0 στην αριστερή πλευρά της εξίσωσης, όπως στο προηγούμενο παράδειγμα:

Προφανώς, σε αυτή την περίπτωση θα υπάρχουν δύο μηδενικά της συνάρτησης: x=3 και x=-3. Εάν η εξίσωση είχε όρισμα τρίτου βαθμού, θα υπήρχαν τρία μηδενικά. Ένα απλό συμπέρασμα μπορεί να εξαχθεί ότι ο αριθμός των ριζών του πολυωνύμου αντιστοιχεί στον μέγιστο βαθμό του επιχειρήματος στην εξίσωση. Ωστόσο, πολλές συναρτήσεις, για παράδειγμα y = x 3, με την πρώτη ματιά έρχονται σε αντίθεση με αυτή τη δήλωση. Η λογική και η κοινή λογική υπαγορεύουν ότι αυτή η συνάρτηση έχει μόνο ένα μηδέν - στο σημείο x=0. Αλλά στην πραγματικότητα υπάρχουν τρεις ρίζες, απλώς συμπίπτουν όλες. Εάν λύσετε την εξίσωση σε μιγαδική μορφή, αυτό γίνεται προφανές. x=0 σε αυτή την περίπτωση, μια ρίζα της οποίας ο πολλαπλασιασμός είναι 3. Στο προηγούμενο παράδειγμα, τα μηδενικά δεν συμπίπτουν, επομένως είχαν πολλαπλότητα 1.

Αλγόριθμος προσδιορισμού

Από τα παραδείγματα που παρουσιάζονται μπορείτε να δείτε πώς να προσδιορίσετε τα μηδενικά μιας συνάρτησης. Ο αλγόριθμος είναι πάντα ο ίδιος:

1. Γράψτε μια συνάρτηση.
2. Αντικαταστήστε το y ή f(x)=0.
3. Λύστε την εξίσωση που προκύπτει.

Η δυσκολία του τελευταίου σημείου εξαρτάται από το βαθμό του επιχειρήματος της εξίσωσης. Κατά την επίλυση εξισώσεων υψηλών βαθμών, είναι ιδιαίτερα σημαντικό να θυμάστε ότι ο αριθμός των ριζών της εξίσωσης είναι ίσος με τον μέγιστο βαθμό του επιχειρήματος. Αυτό ισχύει ιδιαίτερα για τις τριγωνομετρικές εξισώσεις, όπου η διαίρεση και των δύο πλευρών με ημίτονο ή συνημίτονο οδηγεί σε απώλεια ριζών.

Οι εξισώσεις αυθαίρετου βαθμού επιλύονται ευκολότερα χρησιμοποιώντας τη μέθοδο του Horner, η οποία αναπτύχθηκε ειδικά για την εύρεση των μηδενικών ενός αυθαίρετου πολυωνύμου.

Η τιμή των μηδενικών συναρτήσεων μπορεί να είναι είτε αρνητική είτε θετική, πραγματική ή στο μιγαδικό επίπεδο, ενική ή πολλαπλή. Ή μπορεί να μην υπάρχουν ρίζες στην εξίσωση. Για παράδειγμα, η συνάρτηση y=8 δεν θα αποκτήσει μηδενική τιμή για οποιοδήποτε x, επειδή δεν εξαρτάται από αυτή τη μεταβλητή.

Η εξίσωση y=x 2 -16 έχει δύο ρίζες, και οι δύο βρίσκονται στο μιγαδικό επίπεδο: x 1 =4i, x 2 =-4i.

Κοινά λάθη

Ένα συνηθισμένο λάθος που κάνουν οι μαθητές που δεν έχουν ακόμη κατανοήσει πλήρως τι είναι τα μηδενικά μιας συνάρτησης είναι η αντικατάσταση του ορίσματος (x) με μηδέν, αντί της τιμής (y) της συνάρτησης. Αντικαθιστούν με σιγουριά το x=0 στην εξίσωση και, με βάση αυτό, βρίσκουν το y. Αλλά αυτή είναι η λάθος προσέγγιση.

Ένα άλλο λάθος, όπως ήδη αναφέρθηκε, είναι η αναγωγή με ημίτονο ή συνημίτονο σε μια τριγωνομετρική εξίσωση, γι' αυτό χάνονται ένα ή περισσότερα μηδενικά της συνάρτησης. Αυτό δεν σημαίνει ότι τίποτα δεν μπορεί να μειωθεί σε τέτοιες εξισώσεις, αλλά σε περαιτέρω υπολογισμούς είναι απαραίτητο να ληφθούν υπόψη αυτοί οι «χαμένοι» παράγοντες.

ΓΡΑΦΙΚΗ ΑΝΑΠΑΡΑΣΤΑΣΗ

Μπορείτε να καταλάβετε τι είναι τα μηδενικά μιας συνάρτησης χρησιμοποιώντας μαθηματικά προγράμματα όπως το Maple. Μπορείτε να δημιουργήσετε ένα γράφημα σε αυτό καθορίζοντας τον επιθυμητό αριθμό σημείων και την επιθυμητή κλίμακα. Εκείνα τα σημεία στα οποία το γράφημα τέμνει τον άξονα OX είναι τα επιθυμητά μηδενικά. Αυτός είναι ένας από τους πιο γρήγορους τρόπους για να βρείτε τις ρίζες ενός πολυωνύμου, ειδικά εάν η σειρά του είναι μεγαλύτερη από την τρίτη. Έτσι, εάν υπάρχει ανάγκη να εκτελείτε τακτικά μαθηματικούς υπολογισμούς, να βρείτε τις ρίζες πολυωνύμων αυθαίρετων βαθμών, να δημιουργήσετε γραφήματα, το Maple ή ένα παρόμοιο πρόγραμμα θα είναι απλώς απαραίτητο για την εκτέλεση και τον έλεγχο υπολογισμών.

2. Ας βρούμε τα μηδενικά της συνάρτησης.

f(x) στο x .

Απαντήστε f(x) στο x .

2) x 2 >-4x-5;

x 2 +4x +5>0;

Έστω f(x)=x 2 +4x +5, τότε ας βρούμε τέτοιο x για το οποίο f(x)>0,

D=-4 Χωρίς μηδενικά.

4. Συστήματα ανισοτήτων. Ανισότητες και συστήματα ανισοτήτων με δύο μεταβλητές

1) Το σύνολο λύσεων σε ένα σύστημα ανισώσεων είναι η τομή των συνόλων λύσεων στις ανισότητες που περιλαμβάνονται σε αυτό.

2) Το σύνολο των λύσεων της ανισότητας f(x;y)>0 μπορεί να απεικονιστεί γραφικά στο επίπεδο συντεταγμένων. Τυπικά, η ευθεία που ορίζεται από την εξίσωση f(x;y) = 0 διαιρεί το επίπεδο σε 2 μέρη, ένα από τα οποία είναι η λύση της ανισότητας. Για να προσδιορίσετε ποιο μέρος, πρέπει να αντικαταστήσετε τις συντεταγμένες ενός αυθαίρετου σημείου M(x0;y0) που δεν βρίσκεται στην ευθεία f(x;y)=0 στην ανισότητα. Αν f(x0;y0) > 0, τότε η λύση της ανισότητας είναι το τμήμα του επιπέδου που περιέχει το σημείο M0. αν f(x0;y0)<0, то другая часть плоскости.

3) Το σύνολο λύσεων σε ένα σύστημα ανισώσεων είναι η τομή των συνόλων λύσεων στις ανισότητες που περιλαμβάνονται σε αυτό. Ας δοθεί, για παράδειγμα, ένα σύστημα ανισοτήτων:

.

Για την πρώτη ανισότητα, το σύνολο των λύσεων είναι ένας κύκλος ακτίνας 2 και έχει κέντρο στην αρχή και για τη δεύτερη είναι ένα ημιεπίπεδο που βρίσκεται πάνω από την ευθεία 2x+3y=0. Το σύνολο των λύσεων αυτού του συστήματος είναι η τομή αυτών των συνόλων, δηλ. ημικύκλιο.

4) Παράδειγμα. Λύστε το σύστημα των ανισοτήτων:

Η λύση στην 1η ανισότητα είναι το σύνολο , η 2η είναι το σύνολο (2;7) και η τρίτη είναι το σύνολο .

Η τομή αυτών των συνόλων είναι το διάστημα (2;3], το οποίο είναι το σύνολο των λύσεων στο σύστημα των ανισοτήτων.

5. Επίλυση ορθολογικών ανισώσεων με τη μέθοδο του διαστήματος

Η μέθοδος των διαστημάτων βασίζεται στην ακόλουθη ιδιότητα του διωνύμου (x-a): το σημείο x = α διαιρεί τον αριθμητικό άξονα σε δύο μέρη - στα δεξιά του σημείου α το διώνυμο (x-α)>0, και στο αριστερά από το σημείο α (x-α)<0.

Έστω απαραίτητο να λυθεί η ανίσωση (x-α 1)(x-α 2)...(x-α n)>0, όπου α 1, α 2 ...α n-1, α n είναι σταθερά αριθμοί, μεταξύ των οποίων δεν υπάρχουν ίσοι, και τέτοιοι ώστε α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 χρησιμοποιώντας τη μέθοδο του διαστήματος προχωρήστε ως εξής: οι αριθμοί α 1, α 2 ...α n-1, α n απεικονίζονται στον αριθμητικό άξονα. στο διάστημα στα δεξιά του μεγαλύτερου από αυτά, δηλ. αριθμοί α n, βάλτε πρόσημο συν, στο διάστημα που ακολουθεί από δεξιά προς τα αριστερά βάλτε πρόσημο μείον, μετά συν, μετά αρνητικό κ.λπ. Τότε το σύνολο όλων των λύσεων στην ανίσωση (x-α 1)(x‑α 2)...(x-α n)>0 θα είναι η ένωση όλων των διαστημάτων στα οποία τοποθετείται το σύμβολο συν και το σύνολο των λύσεων της ανισότητας (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) Επίλυση ορθολογικών ανισοτήτων (δηλαδή ανισώσεων της μορφής Το P(x) Q(x) όπου είναι πολυώνυμα) βασίζεται στην ακόλουθη ιδιότητα μιας συνεχούς συνάρτησης: εάν μια συνεχής συνάρτηση εξαφανίζεται στα σημεία x1 και x2 (x1; x2) και δεν έχει άλλες ρίζες μεταξύ αυτών των σημείων, τότε στο διαστήματα (x1; x2) η συνάρτηση διατηρεί το πρόσημό της.

Επομένως, για να βρείτε διαστήματα σταθερού πρόσημου της συνάρτησης y=f(x) στην αριθμητική ευθεία, σημειώστε όλα τα σημεία στα οποία η συνάρτηση f(x) εξαφανίζεται ή υφίσταται ασυνέχεια. Αυτά τα σημεία διαιρούν την αριθμητική γραμμή σε πολλά διαστήματα, μέσα σε καθένα από τα οποία η συνάρτηση f(x) είναι συνεχής και δεν εξαφανίζεται, δηλ. σώζει το σημάδι. Για να προσδιορίσετε αυτό το πρόσημο, αρκεί να βρείτε το πρόσημο της συνάρτησης σε οποιοδήποτε σημείο του εξεταζόμενου διαστήματος της αριθμογραμμής.

2) Να προσδιορίζει διαστήματα σταθερού πρόσημου μιας ορθολογικής συνάρτησης, δηλ. Για να λύσουμε μια ορθολογική ανισότητα, σημειώνουμε στην αριθμητική γραμμή τις ρίζες του αριθμητή και τις ρίζες του παρονομαστή, που είναι επίσης οι ρίζες και τα σημεία διακοπής της ορθολογικής συνάρτησης.

Επίλυση ανισώσεων με τη μέθοδο του διαστήματος

3. < 20.

Λύση. Το εύρος των αποδεκτών τιμών καθορίζεται από το σύστημα των ανισοτήτων:

Για τη συνάρτηση f(x) = – 20. Βρείτε f(x):

από όπου x = 29 και x = 13.

f(30) = – 20 = 0,3 > 0,

f(5) = – 1 – 20 = – 10< 0.

Απάντηση: . Βασικές μέθοδοι επίλυσης ορθολογικών εξισώσεων. 1) Το απλούστερο: λύνεται με τις συνήθεις απλοποιήσεις - αναγωγή σε κοινό παρονομαστή, αναγωγή παρόμοιων όρων κ.λπ. Οι δευτεροβάθμιες εξισώσεις ax2 + bx + c = 0 λύνονται με...

Το X αλλάζει στο διάστημα (0,1] και μειώνεται στο διάστημα .

Βλέπουμε ότι προσθέτουμε nστο επιχείρημα Χ, δεν αλλάζει

τιμή συνάρτησης. Ο μικρότερος μη μηδενικός αριθμός

από nείναι , άρα αυτή είναι η περίοδος αμαρτία 2 Χ .

Συναρτήσεις μηδενικά. Καλείται η τιμή ορίσματος στην οποία η συνάρτηση είναι ίση με 0 μηδέν ( ρίζα) συνάρτηση. Μια συνάρτηση μπορεί να έχει πολλαπλά μηδενικά. Για παράδειγμα, η συνάρτηση y = Χ (Χ + 1) (Χ- 3) έχει τρία μηδενικά: Χ = 0, Χ = — 1, Χ= 3. Γεωμετρικά μηδενική συνάρτηση – αυτή είναι η τετμημένη του σημείου τομής της γραφικής παράστασης συνάρτησης με τον άξονα Χ .

Το σχήμα 7 δείχνει ένα γράφημα μιας συνάρτησης με μηδενικά: Χ = ένα , Χ = σιΚαι Χ = ντο .

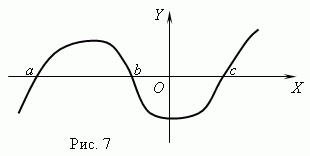
Ασύμπτωτο. Εάν η γραφική παράσταση μιας συνάρτησης πλησιάζει απεριόριστα μια συγκεκριμένη γραμμή καθώς απομακρύνεται από την αρχή, τότε αυτή η γραμμή ονομάζεται ασύμπτωτο.

Θέμα 6. «Μέθοδος διαστήματος».

Αν f (x) f (x 0) για x x 0, τότε καλείται η συνάρτηση f (x). συνεχής στο σημείο x 0.

Αν μια συνάρτηση είναι συνεχής σε κάθε σημείο κάποιου διαστήματος I, τότε καλείται συνεχής στο διάστημα I (το διάστημα I ονομάζεται διάστημα συνέχειας της συνάρτησης). Το γράφημα μιας συνάρτησης σε αυτό το διάστημα είναι μια συνεχής γραμμή, η οποία λένε ότι μπορεί να "σχεδιαστεί χωρίς να σηκωθεί το μολύβι από το χαρτί".

Ιδιότητα συνεχών συναρτήσεων.

Εάν στο διάστημα (a ; b) η συνάρτηση f είναι συνεχής και δεν εξαφανίζεται, τότε διατηρεί ένα σταθερό πρόσημο σε αυτό το διάστημα.

Σε αυτήν την ιδιότητα βασίζεται μια μέθοδος επίλυσης ανισώσεων με μία μεταβλητή, η μέθοδος διαστήματος. Έστω η συνάρτηση f(x) συνεχής στο διάστημα I και εξαφανίζεται σε έναν πεπερασμένο αριθμό σημείων σε αυτό το διάστημα. Με την ιδιότητα των συνεχών συναρτήσεων, αυτά τα σημεία χωρίζουν το I σε διαστήματα, σε καθένα από τα οποία η συνεχής συνάρτηση f(x) c διατηρεί σταθερό πρόσημο. Για να προσδιοριστεί αυτό το πρόσημο, αρκεί να υπολογίσουμε την τιμή της συνάρτησης f(x) σε οποιοδήποτε σημείο από κάθε τέτοιο διάστημα. Με βάση αυτό, λαμβάνουμε τον ακόλουθο αλγόριθμο για την επίλυση ανισώσεων με τη μέθοδο του διαστήματος.

Μέθοδος διαστήματος για ανισώσεις της μορφής

Να βρείτε το πεδίο ορισμού της συνάρτησης f(x) ;

Να βρείτε τα μηδενικά της συνάρτησης f(x) ;

Σχεδιάστε το πεδίο ορισμού και τα μηδενικά της συνάρτησης στην αριθμητική γραμμή. Τα μηδενικά μιας συνάρτησης διαιρούν το πεδίο ορισμού της σε διαστήματα, σε καθένα από τα οποία η συνάρτηση διατηρεί ένα σταθερό πρόσημο.

Βρείτε τα πρόσημα της συνάρτησης στα διαστήματα που προκύπτουν υπολογίζοντας την τιμή της συνάρτησης σε οποιοδήποτε σημείο από κάθε διάστημα.

Γράψτε την απάντηση.

Μέθοδος διαστήματος. Μέσο επίπεδο.

Θέλετε να δοκιμάσετε τη δύναμή σας και να μάθετε το αποτέλεσμα του πόσο έτοιμοι είστε για τις εξετάσεις Unified State Exam ή Unified State Exam;

Γραμμική συνάρτηση

Μια συνάρτηση της φόρμας ονομάζεται γραμμική. Ας πάρουμε μια συνάρτηση ως παράδειγμα. Είναι θετικό στο 3″> και αρνητικό στο. Η τελεία είναι το μηδέν της συνάρτησης (). Ας δείξουμε τα σημάδια αυτής της συνάρτησης στον αριθμητικό άξονα:

Λέμε ότι «η συνάρτηση αλλάζει πρόσημο όταν διέρχεται από το σημείο».

Μπορεί να φανεί ότι τα πρόσημα της συνάρτησης αντιστοιχούν στη θέση του γραφήματος συνάρτησης: εάν το γράφημα είναι πάνω από τον άξονα, το πρόσημο είναι « », αν κάτω από αυτό είναι « ».

Αν γενικεύσουμε τον κανόνα που προκύπτει σε μια αυθαίρετη γραμμική συνάρτηση, έχουμε τον ακόλουθο αλγόριθμο:

Εύρεση του μηδενός της συνάρτησης.

Το σημειώνουμε στον αριθμητικό άξονα.

Προσδιορίζουμε το πρόσημο της συνάρτησης στις απέναντι πλευρές του μηδενός.

Τετραγωνική λειτουργία

Ελπίζω να θυμάστε πώς να λύσετε τις δευτεροβάθμιες ανισότητες; Εάν όχι, διαβάστε το θέμα «Τετραγωνικές ανισότητες». Επιτρέψτε μου να σας υπενθυμίσω τη γενική μορφή μιας τετραγωνικής συνάρτησης: .

Τώρα ας θυμηθούμε τι σημάδια παίρνει η τετραγωνική συνάρτηση. Η γραφική παράσταση της είναι παραβολή και η συνάρτηση παίρνει το πρόσημο " " για εκείνα στα οποία η παραβολή βρίσκεται πάνω από τον άξονα και " " - εάν η παραβολή είναι κάτω από τον άξονα:

Εάν μια συνάρτηση έχει μηδενικά (τιμές στις οποίες), η παραβολή τέμνει τον άξονα σε δύο σημεία - τις ρίζες της αντίστοιχης τετραγωνικής εξίσωσης. Έτσι, ο άξονας χωρίζεται σε τρία διαστήματα και τα σημάδια της συνάρτησης αλλάζουν εναλλάξ όταν διέρχονται από κάθε ρίζα.

Είναι δυνατόν να προσδιορίζονται με κάποιο τρόπο τα σημάδια χωρίς να σχεδιάζετε παραβολή κάθε φορά;

Θυμηθείτε ότι ένα τετράγωνο τριώνυμο μπορεί να παραγοντοποιηθεί:

Ας σημειώσουμε τις ρίζες στον άξονα:

Θυμόμαστε ότι το πρόσημο μιας συνάρτησης μπορεί να αλλάξει μόνο όταν περνά από τη ρίζα. Ας χρησιμοποιήσουμε αυτό το γεγονός: για καθένα από τα τρία διαστήματα στα οποία χωρίζεται ο άξονας με ρίζες, αρκεί να προσδιορίσουμε το πρόσημο της συνάρτησης μόνο σε ένα αυθαίρετα επιλεγμένο σημείο: στα υπόλοιπα σημεία του διαστήματος το πρόσημο θα είναι το ίδιο .

Στο παράδειγμά μας: στο 3″> και οι δύο εκφράσεις στις αγκύλες είναι θετικές (αντικατάσταση, για παράδειγμα: 0″>). Βάζουμε ένα σύμβολο " " στον άξονα:

Λοιπόν, όταν (υποκατάσταση, για παράδειγμα), και οι δύο αγκύλες είναι αρνητικές, πράγμα που σημαίνει ότι το προϊόν είναι θετικό:

Αυτό είναι μέθοδος διαστήματος: γνωρίζοντας τα σημάδια των παραγόντων σε κάθε διάστημα, προσδιορίζουμε το πρόσημο ολόκληρου του προϊόντος.

Ας εξετάσουμε επίσης περιπτώσεις όπου η συνάρτηση δεν έχει μηδενικά ή μόνο ένα.

Αν δεν υπάρχουν, τότε δεν υπάρχουν ρίζες. Αυτό σημαίνει ότι δεν θα υπάρχει «πέρασμα από τη ρίζα». Αυτό σημαίνει ότι η συνάρτηση παίρνει μόνο ένα σύμβολο σε ολόκληρη την αριθμητική γραμμή. Μπορεί εύκολα να προσδιοριστεί αντικαθιστώντας το σε συνάρτηση.

Εάν υπάρχει μόνο μία ρίζα, η παραβολή αγγίζει τον άξονα, οπότε το πρόσημο της συνάρτησης δεν αλλάζει κατά τη διέλευση από τη ρίζα. Τι κανόνα μπορούμε να βγάλουμε για τέτοιες καταστάσεις;

Εάν συνυπολογίσετε μια τέτοια συνάρτηση, λαμβάνετε δύο πανομοιότυπους παράγοντες:

Και οποιαδήποτε τετραγωνισμένη έκφραση είναι μη αρνητική! Επομένως, το πρόσημο της συνάρτησης δεν αλλάζει. Σε τέτοιες περιπτώσεις, θα τονίσουμε τη ρίζα, όταν περνάμε από την οποία το πρόσημο δεν αλλάζει, κυκλώνοντάς την με ένα τετράγωνο:

Θα ονομάσουμε μια τέτοια ρίζα πολλαπλάσια.

Μέθοδος διαστήματος στις ανισώσεις

Τώρα κάθε τετραγωνική ανισότητα μπορεί να λυθεί χωρίς να σχεδιάσουμε παραβολή. Αρκεί απλώς να τοποθετήσετε τα πρόσημα της τετραγωνικής συνάρτησης στον άξονα και να επιλέξετε διαστήματα ανάλογα με το πρόσημο της ανισότητας. Για παράδειγμα:

Ας μετρήσουμε τις ρίζες στον άξονα και ας τοποθετήσουμε τα σημάδια:

Χρειαζόμαστε το τμήμα του άξονα με το σύμβολο " ". Εφόσον η ανισότητα δεν είναι αυστηρή, οι ίδιες οι ρίζες περιλαμβάνονται επίσης στη λύση:

Τώρα εξετάστε μια ορθολογική ανισότητα - μια ανισότητα, της οποίας και οι δύο πλευρές είναι ορθολογικές εκφράσεις (βλ. «Ορθολογικές Εξισώσεις»).

Παράδειγμα:

Όλοι οι παράγοντες εκτός από έναν είναι «γραμμικοί» εδώ, δηλαδή περιέχουν μια μεταβλητή μόνο στην πρώτη δύναμη. Χρειαζόμαστε τέτοιους γραμμικούς παράγοντες για να εφαρμόσουμε τη μέθοδο του διαστήματος - το πρόσημο αλλάζει όταν περνάει από τις ρίζες τους. Αλλά ο πολλαπλασιαστής δεν έχει καθόλου ρίζες. Αυτό σημαίνει ότι είναι πάντα θετικό (ελέγξτε το μόνοι σας) και επομένως δεν επηρεάζει το πρόσημο ολόκληρης της ανισότητας. Αυτό σημαίνει ότι μπορούμε να διαιρέσουμε την αριστερή και τη δεξιά πλευρά της ανισότητας με αυτήν, και έτσι να απαλλαγούμε από αυτήν:

Τώρα όλα είναι ίδια όπως ήταν με τις τετραγωνικές ανισότητες: καθορίζουμε σε ποια σημεία καθένας από τους παράγοντες γίνεται μηδέν, σημειώνουμε αυτά τα σημεία στον άξονα και τακτοποιούμε τα σημάδια. Θα ήθελα να επιστήσω την προσοχή σας σε ένα πολύ σημαντικό γεγονός:

Στην περίπτωση ζυγού αριθμού κάνουμε το ίδιο όπως πριν: κυκλώνουμε το σημείο με τετράγωνο και δεν αλλάζουμε το πρόσημο όταν περνάμε από τη ρίζα. Αλλά στην περίπτωση ενός περιττού αριθμού, αυτός ο κανόνας δεν ισχύει: το πρόσημο θα εξακολουθεί να αλλάζει όταν περνά από τη ρίζα. Επομένως, δεν κάνουμε τίποτα επιπλέον με μια τέτοια ρίζα, σαν να μην είναι πολλαπλάσιο. Οι παραπάνω κανόνες ισχύουν για όλες τις ζυγές και περιττές δυνάμεις.

Τι να γράψουμε στην απάντηση;

Εάν παραβιαστεί η εναλλαγή των ζωδίων, πρέπει να είστε πολύ προσεκτικοί, γιατί εάν η ανισότητα δεν είναι αυστηρή, η απάντηση θα πρέπει να περιλαμβάνει όλα τα σκιασμένα σημεία. Αλλά μερικά από αυτά συχνά ξεχωρίζουν, δηλαδή δεν περιλαμβάνονται στη σκιασμένη περιοχή. Σε αυτήν την περίπτωση, τα προσθέτουμε στην απάντηση ως μεμονωμένα σημεία (σε σγουρά τιράντες):

Παραδείγματα (αποφασίστε μόνοι σας):

Απαντήσεις:

1. Αν μεταξύ των παραγόντων είναι απλός, είναι ρίζα, γιατί μπορεί να αναπαρασταθεί ως.
   .

Στο οποίο παίρνει την τιμή μηδέν. Για παράδειγμα, για μια συνάρτηση που δίνεται από τον τύπο

Είναι μηδέν γιατί

.

Τα μηδενικά μιας συνάρτησης λέγονται επίσης ρίζες της συνάρτησης.

Η έννοια των μηδενικών μιας συνάρτησης μπορεί να ληφθεί υπόψη για οποιεσδήποτε συναρτήσεις των οποίων το εύρος τιμών περιέχει το μηδέν ή το μηδενικό στοιχείο της αντίστοιχης αλγεβρικής δομής.

Για μια συνάρτηση μιας πραγματικής μεταβλητής, μηδενικά είναι οι τιμές στις οποίες το γράφημα της συνάρτησης τέμνει τον άξονα x.

Η εύρεση των μηδενικών μιας συνάρτησης απαιτεί συχνά τη χρήση αριθμητικών μεθόδων (για παράδειγμα, μέθοδος του Νεύτωνα, μέθοδοι κλίσης).

Ένα από τα άλυτα μαθηματικά προβλήματα είναι η εύρεση των μηδενικών της συνάρτησης ζήτα Riemann.

Ρίζα πολυωνύμου

δείτε επίσης

Βιβλιογραφία

Ίδρυμα Wikimedia. 2010.

Δείτε τι είναι το "Function Zero" σε άλλα λεξικά:

Το σημείο όπου μια δεδομένη συνάρτηση f(z) εξαφανίζεται. έτσι, N. f. Η f (z) είναι ίδια με τις ρίζες της εξίσωσης f (z) = 0. Για παράδειγμα, τα σημεία 0, π, π, 2π, 2π,... είναι μηδενικά της συνάρτησης sinz. Μηδενικά μιας αναλυτικής συνάρτησης (Βλ. Αναλυτική... ...

Μηδενική συνάρτηση, μηδενική συνάρτηση... Ορθογραφικό λεξικό-βιβλίο αναφοράς

Αυτός ο όρος έχει άλλες έννοιες, βλέπε Μηδέν. Είναι απαραίτητο να μετακινήσετε τα περιεχόμενα αυτού του άρθρου στο άρθρο "Μηδενική λειτουργία". Μπορείτε να βοηθήσετε το έργο συνδυάζοντας άρθρα. Εάν είναι απαραίτητο να συζητήσουμε τη σκοπιμότητα της συγχώνευσης, αντικαταστήστε αυτό το ... Wikipedia

Ή συμβολοσειρά C (από το όνομα της γλώσσας C) ή συμβολοσειρά ASCIZ (από το όνομα του assembler directive.asciz) μια μέθοδος αναπαράστασης συμβολοσειρών σε γλώσσες προγραμματισμού, στην οποία αντί να εισάγεται ένας ειδικός τύπος συμβολοσειράς, ένας πίνακας χαρακτήρων είναι χρησιμοποιείται, και στο τέλος ... ... Wikipedia

Στην κβαντική θεωρία πεδίου, το αποδεκτό όνομα (ορθολογική) για την ιδιότητα της εξαφάνισης του παράγοντα επανακανονικοποίησης της σταθεράς σύζευξης είναι όπου g0 είναι η σταθερά γυμνής σύζευξης από την αλληλεπίδραση Lagrangian, φυσική. σταθερά σύζευξης ντυμένη ως αλληλεπίδραση. Ισότητα Ζ... Φυσική εγκυκλοπαίδεια

Μηδενική μετάλλαξη ν-αλληλόμορφο- Μηδενική μετάλλαξη, n. αλληλόμορφο * μηδενική μετάλλαξη, n. αλληλόμορφο * μηδενική μετάλλαξη ή n. αλληλόμορφο ή σιωπηλό α. μια μετάλλαξη που οδηγεί σε πλήρη απώλεια της λειτουργίας της αλληλουχίας DNA στην οποία εμφανίστηκε... Γενεσιολογία. εγκυκλοπαιδικό λεξικό

Η δήλωση στη θεωρία πιθανοτήτων ότι οποιοδήποτε γεγονός (το λεγόμενο υπολειπόμενο συμβάν), η εμφάνιση του οποίου καθορίζεται μόνο από αυθαίρετα απομακρυσμένα στοιχεία μιας ακολουθίας ανεξάρτητων τυχαίων γεγονότων ή τυχαίων μεταβλητών, έχει... ... Μαθηματική Εγκυκλοπαίδεια

1) Ένας αριθμός που έχει την ιδιότητα ότι οποιοσδήποτε (πραγματικός ή μιγαδικός) αριθμός δεν αλλάζει όταν προστίθεται σε αυτόν. Συμβολίζεται με το σύμβολο 0. Το γινόμενο οποιουδήποτε αριθμού με Ν. ισούται με Ν.: Αν το γινόμενο δύο αριθμών είναι ίσο με Ν., τότε ένας από τους παράγοντες ... Μαθηματική Εγκυκλοπαίδεια

Συναρτήσεις που ορίζονται από σχέσεις μεταξύ ανεξάρτητων μεταβλητών που δεν επιλύονται σε σχέση με τις τελευταίες. Αυτές οι σχέσεις είναι ένας από τους τρόπους καθορισμού μιας συνάρτησης. Για παράδειγμα, η σχέση x2 + y2 1 = 0 ορίζει το N.f. ... Μεγάλη Σοβιετική Εγκυκλοπαίδεια